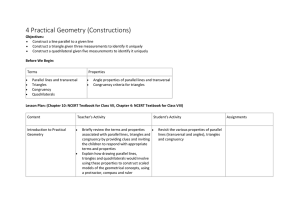
4 Practical Geometry (Constructions) Objectives: Construct a line
... We use various properties of parallel lines, triangles and quadrilaterals to construct these geometrical shapes. This process is a practical reinforcement of various theoretical concepts. e.g. Understanding why three parameters are required to prove congruency of two triangles. Construction is f ...
... We use various properties of parallel lines, triangles and quadrilaterals to construct these geometrical shapes. This process is a practical reinforcement of various theoretical concepts. e.g. Understanding why three parameters are required to prove congruency of two triangles. Construction is f ...
3.1 The concept of parallelism
... began work on the fifth postulate in 1792 while only 15 years old, at first attempting to prove the parallels postulate from the other four. By 1813 he had made little progress and wrote: In the theory of parallels we are even now not further than Euclid. This is a shameful part of mathematics... Ho ...
... began work on the fifth postulate in 1792 while only 15 years old, at first attempting to prove the parallels postulate from the other four. By 1813 he had made little progress and wrote: In the theory of parallels we are even now not further than Euclid. This is a shameful part of mathematics... Ho ...
September 17, 2014
... Show that the diagonals bisect each other Ways to prove that a quadrilateral is a rhombus parallelogram and two adjacent sides congruent parallelogram and perpendicular diagonals parallelogram and diagonals bisect its angles Ways to prove that a quadrilateral is a rectangle parallelogram and one rig ...
... Show that the diagonals bisect each other Ways to prove that a quadrilateral is a rhombus parallelogram and two adjacent sides congruent parallelogram and perpendicular diagonals parallelogram and diagonals bisect its angles Ways to prove that a quadrilateral is a rectangle parallelogram and one rig ...
Chapter 4: Parallels - New Lexington City Schools
... 1. Compare the measures of the alternate interior angles. 2. What is the sum of the measures of the consecutive interior angles? 3. Repeat Steps 1 and 2 above two more times by darkening different pairs of horizontal lines on your paper. Make the transversals intersect the lines at a different angle ...
... 1. Compare the measures of the alternate interior angles. 2. What is the sum of the measures of the consecutive interior angles? 3. Repeat Steps 1 and 2 above two more times by darkening different pairs of horizontal lines on your paper. Make the transversals intersect the lines at a different angle ...
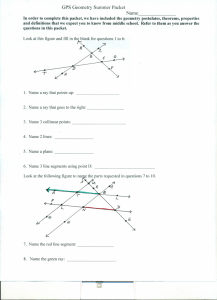
Basic Geometry Terms
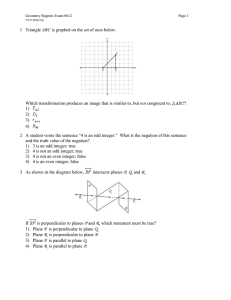
... Corresponding angles are the pairs of angles on the same side of the transversal and on corresponding sides of the two other lines. These angles are equal in degree measure when the two lines intersected by the transversal are parallel. It may help to draw the letter "F" (forwards and backwards) in ...
... Corresponding angles are the pairs of angles on the same side of the transversal and on corresponding sides of the two other lines. These angles are equal in degree measure when the two lines intersected by the transversal are parallel. It may help to draw the letter "F" (forwards and backwards) in ...
Perspective (graphical)

Perspective (from Latin: perspicere to see through) in the graphic arts is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are smaller as their distance from the observer increases; and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight are shorter than its dimensions across the line of sight.Italian Renaissance painters including Paolo Uccello, Piero della Francesca and Luca Pacoima studied linear perspective, wrote treatises on it, and incorporated it into their artworks, thus contributing to the mathematics of art.