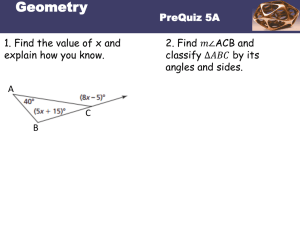
Geometry Curriculum Guide
... perpendicular lines, parallel lines, and line segments. 5) G.CO.5: Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto ...
... perpendicular lines, parallel lines, and line segments. 5) G.CO.5: Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto ...
Euclidean Geometry and History of Non
... parallel line postulate with the postulate that no line may be drawn through a given point, parallel to a given line. Also known as Riemannian geometry. Read more: http://www.answers.com/topic/elliptic-geometry-1#ixzz1n8msBzGE Elliptic geometry (sometimes known as Riemannian geometry) is a non-Eucli ...
... parallel line postulate with the postulate that no line may be drawn through a given point, parallel to a given line. Also known as Riemannian geometry. Read more: http://www.answers.com/topic/elliptic-geometry-1#ixzz1n8msBzGE Elliptic geometry (sometimes known as Riemannian geometry) is a non-Eucli ...
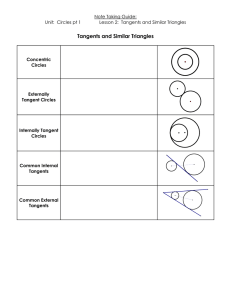
Note Taking Guide
... Tangent Theorem #2: If two segments from the same exterior point are tangent to a circle, then they are congruent. ...
... Tangent Theorem #2: If two segments from the same exterior point are tangent to a circle, then they are congruent. ...
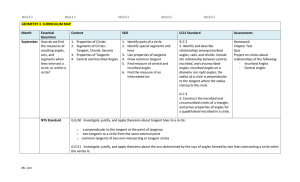
Standards Associated with the unit
... Explain a proof of the Pythagorean Theorem and its converse. Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions. Apply the Pythagorean Theorem to find the distance between two points in a coordinate s ...
... Explain a proof of the Pythagorean Theorem and its converse. Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions. Apply the Pythagorean Theorem to find the distance between two points in a coordinate s ...
MGS43 Geometry 3 Fall Curriculum Map
... transformations as functions that 6. Composition of distance formulas take points in the plane as inputs Transformations ...
... transformations as functions that 6. Composition of distance formulas take points in the plane as inputs Transformations ...
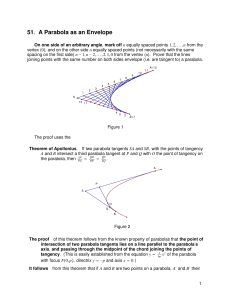
Activity 6.5.2 Cavalieri`s Principle and the Volume of a Sphere
... Activity 6.5.2 Cavalieri’s Principle and the Volume of a Sphere This is a more formal development of the formulas for the volume and surface area of a sphere. Consider a hemisphere with radius r and a cylinder with the same radius and height also equal to r. Inside the cylinder there is a cone with ...
... Activity 6.5.2 Cavalieri’s Principle and the Volume of a Sphere This is a more formal development of the formulas for the volume and surface area of a sphere. Consider a hemisphere with radius r and a cylinder with the same radius and height also equal to r. Inside the cylinder there is a cone with ...
Major arc
... will be able to… • Define and identify arcs and central angles in circles • Calculate the measures of arcs and central angles in circles ...
... will be able to… • Define and identify arcs and central angles in circles • Calculate the measures of arcs and central angles in circles ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.