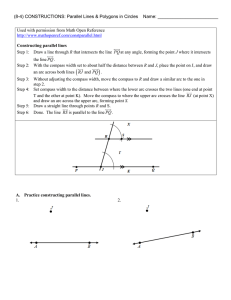
8.5b (build)—Constructing Parallel Lines
... Constructing an equilateral triangle in a circle Start: Start with the line segment AB, which is the length of the sides of the desired equilateral triangle. Step 1: Pick a point P that will be one vertex of the finished triangle. Step 2: Place the point of the compass on the point A and set it's dr ...
... Constructing an equilateral triangle in a circle Start: Start with the line segment AB, which is the length of the sides of the desired equilateral triangle. Step 1: Pick a point P that will be one vertex of the finished triangle. Step 2: Place the point of the compass on the point A and set it's dr ...
Document
... 3. Refer to the diagram to answer each. BE is an angle bisector. a) If mABE = 40, find mEBC. b) If mABC = 70, find mABE. 4. 1 and 2 are complementary. Solve for x and the measure of both angles. ...
... 3. Refer to the diagram to answer each. BE is an angle bisector. a) If mABE = 40, find mEBC. b) If mABC = 70, find mABE. 4. 1 and 2 are complementary. Solve for x and the measure of both angles. ...
Unit 1C: Geometric Reasoning and Proofs
... □ I can use special angles and postulates related to special angles. □ I will calculate the complement and supplement of an angle. □ I will classify adjacent angles, linear pairs, and vertical angles. □ I will classify alternate interior and exterior angles and same side interior and exterior angles ...
... □ I can use special angles and postulates related to special angles. □ I will calculate the complement and supplement of an angle. □ I will classify adjacent angles, linear pairs, and vertical angles. □ I will classify alternate interior and exterior angles and same side interior and exterior angles ...