chapter 2 - pmaguire
... Alternate Exterior Angles Conjecture C-3c (AEA Conjecture) If two parallel lines are cut by a transversal, then alternate exterior angles are _____________. ...
... Alternate Exterior Angles Conjecture C-3c (AEA Conjecture) If two parallel lines are cut by a transversal, then alternate exterior angles are _____________. ...
Identify the transversal connecting each pair of angles. Then classify
... Mid-Chapter Quiz: Lessons 3-1 through 3-3 18. a line parallel to m SOLUTION: The slope of a line parallel to m is same as that of m. The coordinates of two points on the line m are (–10, 0) and (10, –4). Substitute the values in the slope formula. ...
... Mid-Chapter Quiz: Lessons 3-1 through 3-3 18. a line parallel to m SOLUTION: The slope of a line parallel to m is same as that of m. The coordinates of two points on the line m are (–10, 0) and (10, –4). Substitute the values in the slope formula. ...
GCC Unit 8
... o A ________________ is a square if and only if it one _______________________. o A ________________ is a square if and only if it has 2_____________________________________. ...
... o A ________________ is a square if and only if it one _______________________. o A ________________ is a square if and only if it has 2_____________________________________. ...
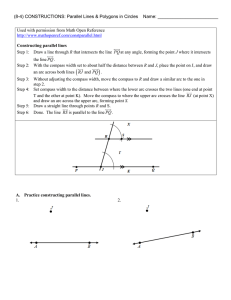
8.5b (build)—Constructing Parallel Lines
... Constructing an equilateral triangle in a circle Start: Start with the line segment AB, which is the length of the sides of the desired equilateral triangle. Step 1: Pick a point P that will be one vertex of the finished triangle. Step 2: Place the point of the compass on the point A and set it's dr ...
... Constructing an equilateral triangle in a circle Start: Start with the line segment AB, which is the length of the sides of the desired equilateral triangle. Step 1: Pick a point P that will be one vertex of the finished triangle. Step 2: Place the point of the compass on the point A and set it's dr ...