Geometry Fall 2014 Lesson 031 _Properties of Parallel Lines
... But this contradicts our previously stated postulate which states through a point not on a given line, there is one and only one line parallel to the given line. Theorem: If two parallel lines are cut by a transversal, then the alternate interior angles formed are congruent. Theorems that are conver ...
... But this contradicts our previously stated postulate which states through a point not on a given line, there is one and only one line parallel to the given line. Theorem: If two parallel lines are cut by a transversal, then the alternate interior angles formed are congruent. Theorems that are conver ...
GEOMETRY CP/HONORS - Verona Public Schools
... radius of a circle is perpendicular to the tangent where the radius intersects the circle. G.C.3 Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle. G.C.4 Construct a tangent line from a point outside a given circ ...
... radius of a circle is perpendicular to the tangent where the radius intersects the circle. G.C.3 Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle. G.C.4 Construct a tangent line from a point outside a given circ ...
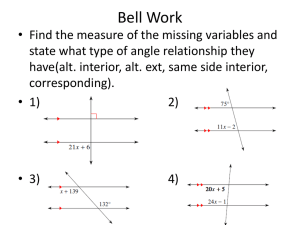
Name: Date: Core-Geometry: 1.4 Angles Warm
... Warm-up: 1. Original price of an unlocked iPhone 5s is 650 USD. In China, the same phone is marked up by 75%. What is the cost in China? (In USD) ...
... Warm-up: 1. Original price of an unlocked iPhone 5s is 650 USD. In China, the same phone is marked up by 75%. What is the cost in China? (In USD) ...
The PAI Postulate:
... The key to proving these relationships is to add some transversals to the diagram so that the PAI Postulate can be used. Here’s the same parallelogram with some lines extended and angle number labels ...
... The key to proving these relationships is to add some transversals to the diagram so that the PAI Postulate can be used. Here’s the same parallelogram with some lines extended and angle number labels ...
Angle-Angle (AA) Similarity Postulate
... Angle-Angle (AA) Similarity Postulate - If two angles of one triangle are CONGRUENT to two angles of another triangle, then the ~o triangles are similar. Why do you NOT need to state that the third pair of angles is congruent when proving the triangles are similar? ...
... Angle-Angle (AA) Similarity Postulate - If two angles of one triangle are CONGRUENT to two angles of another triangle, then the ~o triangles are similar. Why do you NOT need to state that the third pair of angles is congruent when proving the triangles are similar? ...
Prentice Hall Geometry
... 13. Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. [G.CO.13] ...
... 13. Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. [G.CO.13] ...
5/1/16 - Art of Problem Solving
... Jesse Cohen The three medians of a triangle all intersect at a single point which is called the centroid. The centroid divides each median such that the distance from the centroid to the vertex is twice the distance along the median from the centroid to the opposite edge. By applying this to the dia ...
... Jesse Cohen The three medians of a triangle all intersect at a single point which is called the centroid. The centroid divides each median such that the distance from the centroid to the vertex is twice the distance along the median from the centroid to the opposite edge. By applying this to the dia ...