Circles, Arcs and Angles
... Circles and Right Angles The circumcircle for ΔABC exists. Thus, ACB is inscribed in the circle and the arc AB is measured by 2C. C = 90° 2C = 180° AB is a diameter. ...
... Circles and Right Angles The circumcircle for ΔABC exists. Thus, ACB is inscribed in the circle and the arc AB is measured by 2C. C = 90° 2C = 180° AB is a diameter. ...
GEOMETRY E03 RUBRIC
... skew line problems. perpendicular and skew lines. and skew line problems. 2- identify and solve the angles formed by two lines and a ...
... skew line problems. perpendicular and skew lines. and skew line problems. 2- identify and solve the angles formed by two lines and a ...
Standards addressed in Geometry Unit
... B. TSIET model relationship between the volume of a cylinder and a cone having both congruent bases and heights and connect that relationship to the formulas. C. TSIET use models and diagrams to explain the Pythagorean Theorem. (4) 8.b.7 – The student applies mathematical process standards to use ge ...
... B. TSIET model relationship between the volume of a cylinder and a cone having both congruent bases and heights and connect that relationship to the formulas. C. TSIET use models and diagrams to explain the Pythagorean Theorem. (4) 8.b.7 – The student applies mathematical process standards to use ge ...
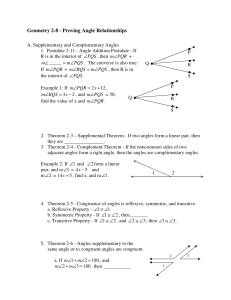
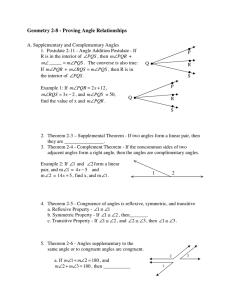
two things are called congruent if they are essentially the same, but
... • All rays are congruent. • All lines are congruent. ...
... • All rays are congruent. • All lines are congruent. ...
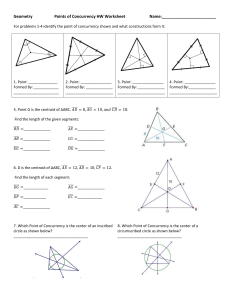
Geometry Points of Concurrency HW Worksheet Name: For
... 9. Which points of concurrency are always inside the triangle? ____________________, __________________ 10. Which point of concurrency is always on the vertex of a right triangle? ______________________________ 11. Which point of concurrency is always on the midpoint of the hypotenuse in a right tri ...
... 9. Which points of concurrency are always inside the triangle? ____________________, __________________ 10. Which point of concurrency is always on the vertex of a right triangle? ______________________________ 11. Which point of concurrency is always on the midpoint of the hypotenuse in a right tri ...
Math Geometry Project Make a 5
... specific geometric terms. Be creative – try to use original pictures (like pointing an arrow to the corner of a cereal box instead of just finding a right angle that you would see in a math textbook). Page/Slide 1: ...
... specific geometric terms. Be creative – try to use original pictures (like pointing an arrow to the corner of a cereal box instead of just finding a right angle that you would see in a math textbook). Page/Slide 1: ...