CST Released Questions
... triangles must be parallel. b. The two triangles must have exactly one d. The corresponding sides of the two acute angle. triangles must be proportional. ____ 20. Which method listed below could not be used to prove that two triangles are congruent? a. Prove all three sets of corresponding sides c. ...
... triangles must be parallel. b. The two triangles must have exactly one d. The corresponding sides of the two acute angle. triangles must be proportional. ____ 20. Which method listed below could not be used to prove that two triangles are congruent? a. Prove all three sets of corresponding sides c. ...
0002_hsm11gmtr_0301.indd
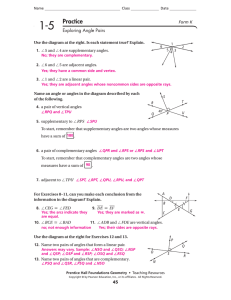
... Use the diagram at the right to answer Exercises 12–15. 12. Name all pairs of corresponding angles. ______________ 13. Name all pairs of alternate interior angles. ____________ 14. Name all pairs of same-side interior angles. ___________ 15. Name all pairs of alternate exterior angles. ____________ ...
... Use the diagram at the right to answer Exercises 12–15. 12. Name all pairs of corresponding angles. ______________ 13. Name all pairs of alternate interior angles. ____________ 14. Name all pairs of same-side interior angles. ___________ 15. Name all pairs of alternate exterior angles. ____________ ...
Lecture 11 - UIUC Math
... • The segment connecting the midpoints of two sides of a triangle is parallel to the third side and half as long. • If a line bisects one side of a triangle and is parallel to a second side, then it bisects the third side and therefore is a midsegment. Applying similarity to our Solar System . . . i ...
... • The segment connecting the midpoints of two sides of a triangle is parallel to the third side and half as long. • If a line bisects one side of a triangle and is parallel to a second side, then it bisects the third side and therefore is a midsegment. Applying similarity to our Solar System . . . i ...