Geometry Module 1, Topic G, Lesson 33: Teacher
... In the first list below, we compile all of the geometric assumptions we took for granted as part of our reasoning and proof-writing process. Though these assumptions were only highlights in lessons, these assumptions form the basis from which all other facts can be derived (e.g., the other facts pre ...
... In the first list below, we compile all of the geometric assumptions we took for granted as part of our reasoning and proof-writing process. Though these assumptions were only highlights in lessons, these assumptions form the basis from which all other facts can be derived (e.g., the other facts pre ...
G-CO.C.9
... Mathematics Curriculum Supplement Geometry (G-CO.C.9) Geometry Mathematics Highly-Leveraged Standard1 G-CO.C.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding ...
... Mathematics Curriculum Supplement Geometry (G-CO.C.9) Geometry Mathematics Highly-Leveraged Standard1 G-CO.C.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding ...
Polygons and Circles
... TIP: Write everything you know onto the drawing, e.g. equilateral triangle - all angles equal 600 before you start. Then write each angle you solve onto the drawing. Supplementary angles equal 1800 ...
... TIP: Write everything you know onto the drawing, e.g. equilateral triangle - all angles equal 600 before you start. Then write each angle you solve onto the drawing. Supplementary angles equal 1800 ...
Sec 4.4 Notes Ans
... Think of points F and Y as two vertices of a triangle. The diver’s entry spot D is the other vertex. You know maF and maY. You also know the length of the included side FY &. From the ASA Congruence Postulate , you can conclude that any two triangles with these measurements are congruent . In other ...
... Think of points F and Y as two vertices of a triangle. The diver’s entry spot D is the other vertex. You know maF and maY. You also know the length of the included side FY &. From the ASA Congruence Postulate , you can conclude that any two triangles with these measurements are congruent . In other ...
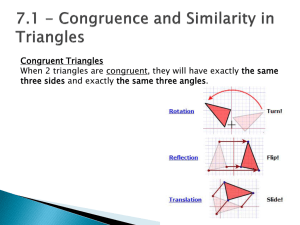
7.1 - Congruence and Similarity in Triangles
... If two triangles are congruent, then they are also similar If two triangles are similar, they are not always congruent If two pairs of corresponding angles in two triangles are equal, then the triangles are similar If in addition two corresponding sides are equal, then the triangles are congruent ...
... If two triangles are congruent, then they are also similar If two triangles are similar, they are not always congruent If two pairs of corresponding angles in two triangles are equal, then the triangles are similar If in addition two corresponding sides are equal, then the triangles are congruent ...
What is covered
... How to study: Study the class notes, solve all the problems we solved in class. Go over the homework problems. If you have time, I also suggest solving the exercises in the “review” part -at the end of the chapters. Below I provided some practice problems for you. This is not a complete list, studyi ...
... How to study: Study the class notes, solve all the problems we solved in class. Go over the homework problems. If you have time, I also suggest solving the exercises in the “review” part -at the end of the chapters. Below I provided some practice problems for you. This is not a complete list, studyi ...