Lesson 4 - Novel Stars
... By the end of this lesson you should understand: ¾ Conditional (if-then) statements ¾ Deduction ¾ Vertical Angle Theorem In this lesson, we are going to learn about conditional statements, deductive reasoning and two-column proofs. These tools are useful in more than just geometry. They also will he ...
... By the end of this lesson you should understand: ¾ Conditional (if-then) statements ¾ Deduction ¾ Vertical Angle Theorem In this lesson, we are going to learn about conditional statements, deductive reasoning and two-column proofs. These tools are useful in more than just geometry. They also will he ...
Geometry Ch 2 and 3 Assignment Log Gordon
... must perform the skill perfectly two times. All students will have the opportunity to take a target quiz three times during class and their best score will prevail. If after the three opportunities a student has not demonstrated they understand the target, it is up to the student to arrange a time b ...
... must perform the skill perfectly two times. All students will have the opportunity to take a target quiz three times during class and their best score will prevail. If after the three opportunities a student has not demonstrated they understand the target, it is up to the student to arrange a time b ...
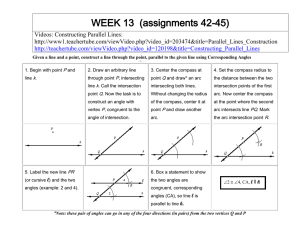
2.5 Proving Angles Congruent SWBAT…
... Adjacent angles: two coplanar angels with a common side, a common vertex, and no common interior points. Complementary angles: two angles whose measures have sum 90 Supplementary angels: two angles whose measures have sum of 180 ...
... Adjacent angles: two coplanar angels with a common side, a common vertex, and no common interior points. Complementary angles: two angles whose measures have sum 90 Supplementary angels: two angles whose measures have sum of 180 ...