Domain of sin(x) , cos(x) is R. Domain of tan(x) is R \ {(k + 2)π : k ∈ Z
... We obtain the equation for g(x) by solving f (x) = y for x, then we get an expression g(y) = x, and then we simply replace x by y. This means that the graph of the inverse fuinction g(x) can be obtained from the graph of f (x) by reflecting it about the line with equation y = x. This can be seen in ...
... We obtain the equation for g(x) by solving f (x) = y for x, then we get an expression g(y) = x, and then we simply replace x by y. This means that the graph of the inverse fuinction g(x) can be obtained from the graph of f (x) by reflecting it about the line with equation y = x. This can be seen in ...
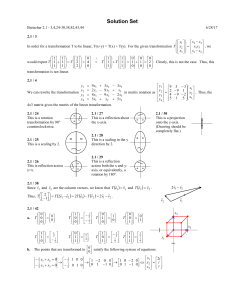
Review of Wednesday`s Lecture
... Product Term Single literal or a product of literals (a, abc’) Sum of Products Expression (SOP) Logical sum of two or more products (ab + cd) Sum term Single literal or a sum of literals (a, a+b+c) Product of Sums Expression (POS) Logical product of two or more sums (a+b+c)(a+b') Normal Term a produ ...
... Product Term Single literal or a product of literals (a, abc’) Sum of Products Expression (SOP) Logical sum of two or more products (ab + cd) Sum term Single literal or a sum of literals (a, a+b+c) Product of Sums Expression (POS) Logical product of two or more sums (a+b+c)(a+b') Normal Term a produ ...
tutorial1
... Once a coordinate system is fixed, we can locate any point in the universe with a 3x1 position vector. The components of P in {A} have numerical values which indicate distances along the axes of {A}. To describe the orientation of a body we will attach a coordinate system to the body and then give a ...
... Once a coordinate system is fixed, we can locate any point in the universe with a 3x1 position vector. The components of P in {A} have numerical values which indicate distances along the axes of {A}. To describe the orientation of a body we will attach a coordinate system to the body and then give a ...
Differential geometric formulation of Maxwell`s equations
... exterior product of k variables by exterior product of the complementary set of n − k variables (up to a constant factor, which depends on the metric tensor and the order of the variables in the two products). More precisely, let σ = (i1 , i2 , . . . , in ) be a permutation of (1, 2, . . . , n); the ...
... exterior product of k variables by exterior product of the complementary set of n − k variables (up to a constant factor, which depends on the metric tensor and the order of the variables in the two products). More precisely, let σ = (i1 , i2 , . . . , in ) be a permutation of (1, 2, . . . , n); the ...
8-7 Practice: Vectors
... 8. AVIATION A jet begins a flight along a path due north at 300 miles per hour. A wind is blowing due west at 30 miles per hour. a. Find the resultant velocity of the plane. b. Find the resultant direction of the plane. ...
... 8. AVIATION A jet begins a flight along a path due north at 300 miles per hour. A wind is blowing due west at 30 miles per hour. a. Find the resultant velocity of the plane. b. Find the resultant direction of the plane. ...
Document
... The w-coordinate of V determines whether V is a point or a direction vector If w = 0, then V is a direction vector and the fourth column of the transformation ...
... The w-coordinate of V determines whether V is a point or a direction vector If w = 0, then V is a direction vector and the fourth column of the transformation ...
Norm and inner products in Rn Math 130 Linear Algebra
... 2 since we know a lot of plane geometry. kvk2 = v12 + v22 + · · · + vn2 , The law of cosines for oblique triangles says that given a triangle with sides a, b, and c, and angle θ therefore between sides a and b, kvk2 = hv|vi. Because of this connection between norm and inner product, we can often red ...
... 2 since we know a lot of plane geometry. kvk2 = v12 + v22 + · · · + vn2 , The law of cosines for oblique triangles says that given a triangle with sides a, b, and c, and angle θ therefore between sides a and b, kvk2 = hv|vi. Because of this connection between norm and inner product, we can often red ...
Cross product
In mathematics and vector calculus, the cross product or vector product (occasionally directed area product to emphasize the geometric significance) is a binary operation on two vectors in three-dimensional space (R3) and is denoted by the symbol ×. The cross product a × b of two linearly independent vectors a and b is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with dot product (projection product).If two vectors have the same direction (or have the exact opposite direction from one another, i.e. are not linearly independent) or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The cross product is anticommutative (i.e. a × b = −b × a) and is distributive over addition (i.e. a × (b + c) = a × b + a × c). The space R3 together with the cross product is an algebra over the real numbers, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on a choice of orientation or ""handedness"". The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions. If one adds the further requirement that the product be uniquely defined, then only the 3-dimensional cross product qualifies. (See § Generalizations, below, for other dimensions.)