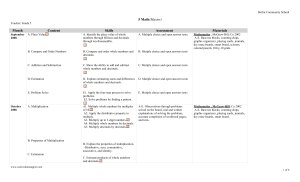
By the end of grade 3, students will be able to:
... 24. Routinely use the skills learned in math class at other times during the school day. 25. Appreciate and use their knowledge of numbers in situations outside the classroom. By the end of grade 2, students will be able to: 1. Demonstrate an understanding of the concept of place value using various ...
... 24. Routinely use the skills learned in math class at other times during the school day. 25. Appreciate and use their knowledge of numbers in situations outside the classroom. By the end of grade 2, students will be able to: 1. Demonstrate an understanding of the concept of place value using various ...
Types of Numbers - English for Maths
... A number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n. An abundant number is a number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n. Abundant numbers are part of the famil ...
... A number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n. An abundant number is a number n for which the sum of divisors σ(n)>2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)>n. Abundant numbers are part of the famil ...
Math 7A Unit 1
... 3) How many numbers have an absolute value of 12? ______ List them. _______________ 4) The counting numbers are _____________________. 5) The whole numbers are ALL the ____________________ and ____________. 6) The integers are ALL the _______________ and their _________________. For 7-12 state wheth ...
... 3) How many numbers have an absolute value of 12? ______ List them. _______________ 4) The counting numbers are _____________________. 5) The whole numbers are ALL the ____________________ and ____________. 6) The integers are ALL the _______________ and their _________________. For 7-12 state wheth ...
log
... Hint: Samreen has used the statement of the theorem "Let x = p/q be a rational number, such that the prime factorization of q is of the form 2n 5m where n, m are non-negative integers. Then x has a decimal expansion which terminates". ...
... Hint: Samreen has used the statement of the theorem "Let x = p/q be a rational number, such that the prime factorization of q is of the form 2n 5m where n, m are non-negative integers. Then x has a decimal expansion which terminates". ...
Maths medium term plan: autumn term
... number using the formal written method of long multiplication Divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context Divide numbers up t ...
... number using the formal written method of long multiplication Divide numbers up to 4 digits by a two-digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context Divide numbers up t ...
Section 1.4 Proving Conjectures: Deductive Reasoning
... (A)All natural numbers are whole numbers. All whole numbers are integers. 3 is a natural number. What can be deduced about the number 3? ...
... (A)All natural numbers are whole numbers. All whole numbers are integers. 3 is a natural number. What can be deduced about the number 3? ...
Why i? The Historical Roots of “Imaginary” Numbers The first
... began to view complex numbers as points in the plane: that is, a complex number is a number of the form z = x + iy and z can be represented as the point (x, y ) in the plane. Euler’s equation helped considerably both in leading to this geometric viewpoint and in the understanding of the basic arithm ...
... began to view complex numbers as points in the plane: that is, a complex number is a number of the form z = x + iy and z can be represented as the point (x, y ) in the plane. Euler’s equation helped considerably both in leading to this geometric viewpoint and in the understanding of the basic arithm ...
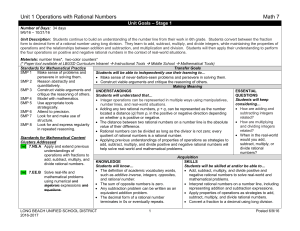
Unit 1 Operations with Rational Numbers Math 7
... Students will complete selected response and constructed response items to indicate level of mastery/understanding of the unit standards as outlined in this guide. [m] 7.NS.A • The student interprets rational number values on a number line, including representations of addition and subtraction expre ...
... Students will complete selected response and constructed response items to indicate level of mastery/understanding of the unit standards as outlined in this guide. [m] 7.NS.A • The student interprets rational number values on a number line, including representations of addition and subtraction expre ...
complex numbers - Siby Sebastian
... Historically, the geometric representation of a complex number as a point in the plane was important because it made the whole idea of a complex number more acceptable. In particular, this visualization helped "imaginary" and "complex" numbers become accepted in mainstream mathematics as a natural e ...
... Historically, the geometric representation of a complex number as a point in the plane was important because it made the whole idea of a complex number more acceptable. In particular, this visualization helped "imaginary" and "complex" numbers become accepted in mainstream mathematics as a natural e ...
Leonhard Euler - UT Mathematics
... • Question 1—Is there a way to visit each land mass using a bridge only once? (Eulerian path) • Question 2—Is there a way to visit each land mass using a bridge only once and beginning and arriving at the same point? (Eulerian circuit) ...
... • Question 1—Is there a way to visit each land mass using a bridge only once? (Eulerian path) • Question 2—Is there a way to visit each land mass using a bridge only once and beginning and arriving at the same point? (Eulerian circuit) ...
The Fibonacci Sequence
... The Fibonacci numbers first appeared in the 6th century AD with the Indian mathematician Virahanka’s analysis of metres with long and short syllables. In the West, the sequence was first studied by Leonardo of Pisa, known as Fibonacci, in his Liber Abaci (1202). The Fibonacci numbers are the product ...
... The Fibonacci numbers first appeared in the 6th century AD with the Indian mathematician Virahanka’s analysis of metres with long and short syllables. In the West, the sequence was first studied by Leonardo of Pisa, known as Fibonacci, in his Liber Abaci (1202). The Fibonacci numbers are the product ...