Document
... fans are rooting for the home team. What fraction of the bleacher is rooting for the home team? ...
... fans are rooting for the home team. What fraction of the bleacher is rooting for the home team? ...
Unit 13(Playing With Numbers)
... 32. If B × B = AB, then either A = 2, B = 5 or A = ______, B = ______. 33. If the digit 1 is placed after a 2-digit number whose tens is t and ones digit is u, the new number is ______. State whether the statements given in questions 34 to 44 are true (T) or false (F): 34. A two-digit number ab is a ...
... 32. If B × B = AB, then either A = 2, B = 5 or A = ______, B = ______. 33. If the digit 1 is placed after a 2-digit number whose tens is t and ones digit is u, the new number is ______. State whether the statements given in questions 34 to 44 are true (T) or false (F): 34. A two-digit number ab is a ...
MMS 5
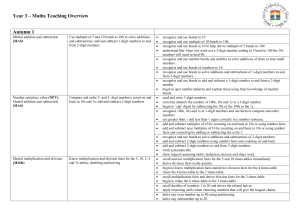
... Solve length puzzles by calculating diameters and side lengths Use grids for products of 3-digit and 2-digit numbers (both large numbers and decimal fractions) for rows of circles and squares Recognise and write values of vertically opposite, corresponding and opposite angles in a parallelogra ...
... Solve length puzzles by calculating diameters and side lengths Use grids for products of 3-digit and 2-digit numbers (both large numbers and decimal fractions) for rows of circles and squares Recognise and write values of vertically opposite, corresponding and opposite angles in a parallelogra ...
39(1)
... The Ninth International Conference on Fibonacci Numbers and Their Applications was held in Luxembourg 17-22 July 2000. It was the first conference without our dear Herta Freitag, who died on 25 January 2000. Herta graced every one of our previous eight conferences with her warm and friendly presence ...
... The Ninth International Conference on Fibonacci Numbers and Their Applications was held in Luxembourg 17-22 July 2000. It was the first conference without our dear Herta Freitag, who died on 25 January 2000. Herta graced every one of our previous eight conferences with her warm and friendly presence ...
odd and even numbers - KCPE-KCSE
... Greek letter π is often used in exam questions to represent a constant ...
... Greek letter π is often used in exam questions to represent a constant ...
Rational number - amans maths blogs
... –2 and vice-versa. In general, for an integer a, we have, a + (– a) = (– a) + a = 0; so, a is the negative of – a and – a is the negative of a. ...
... –2 and vice-versa. In general, for an integer a, we have, a + (– a) = (– a) + a = 0; so, a is the negative of – a and – a is the negative of a. ...
Rational Numbers
... –2 and vice-versa. In general, for an integer a, we have, a + (– a) = (– a) + a = 0; so, a is the negative of – a and – a is the negative of a. ...
... –2 and vice-versa. In general, for an integer a, we have, a + (– a) = (– a) + a = 0; so, a is the negative of – a and – a is the negative of a. ...
Simulations of Sunflower Spirals and Fibonacci Numbers
... simulations values of V are chosen so that points are not crowded too much. An example to draw spirals on a real sunflower is shown in Fig. 4, where three kinked curves are drawn. We can see 89, 55, 34, 21 spirals in the layers (from outer to inner), while spirals in the fifth layer are difficult to ...
... simulations values of V are chosen so that points are not crowded too much. An example to draw spirals on a real sunflower is shown in Fig. 4, where three kinked curves are drawn. We can see 89, 55, 34, 21 spirals in the layers (from outer to inner), while spirals in the fifth layer are difficult to ...
Sums of Two Triangulars and of Two Squares Associated with Sum
... Notice that only three (8n! + 1) from the list in Table 2 can be represented as a square. In addition, by examining the end digits of both factorial and triangular numbers it can be deduced that Ft n = Tx + Tn or n! x( x 1) / 2 is true only if, x belongs to any of the sequences {15, 35, 55, 75, ...
... Notice that only three (8n! + 1) from the list in Table 2 can be represented as a square. In addition, by examining the end digits of both factorial and triangular numbers it can be deduced that Ft n = Tx + Tn or n! x( x 1) / 2 is true only if, x belongs to any of the sequences {15, 35, 55, 75, ...
divisibility rules
... 144 : ends in a 4 and adds up to 9 therefore 144 can be divided by 6. 154 : ends in a 4 but adds up to 10 therefore 154 can not be divided by 6. because you can’t divided it by 3. ...
... 144 : ends in a 4 and adds up to 9 therefore 144 can be divided by 6. 154 : ends in a 4 but adds up to 10 therefore 154 can not be divided by 6. because you can’t divided it by 3. ...
Introduction to Floating-point Numbers
... – We have a problem for which we are looking for a solution x* – We start with an initial approximation or guess, call it x0 – We develop an algorithm or formula that takes a given approximation xk and hopefully produces a better approximation xk + 1 of x* – We need mechanisms to indicate: • When ou ...
... – We have a problem for which we are looking for a solution x* – We start with an initial approximation or guess, call it x0 – We develop an algorithm or formula that takes a given approximation xk and hopefully produces a better approximation xk + 1 of x* – We need mechanisms to indicate: • When ou ...