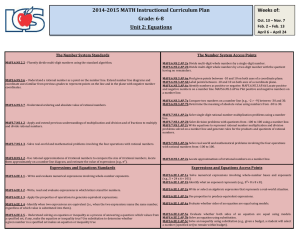
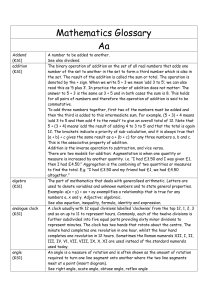
Floating point unit demonstration on STM32
... Picture of Mandelbrot-set using Double precision FPU with zoom in 48 times. . . . . . . . . . 27 Picture of Mandelbrot-set using Single precision FPU with zoom in 32 times . . . . . . . . . . 27 ...
... Picture of Mandelbrot-set using Double precision FPU with zoom in 48 times. . . . . . . . . . 27 Picture of Mandelbrot-set using Single precision FPU with zoom in 32 times . . . . . . . . . . 27 ...
Chapter 3_3 Properties of Logarithms _Blitzer
... • Multiplication and division are reduced to simple addition and subtraction. • Exponentiation and root operations are reduced to more simple exponent multiplication or division. • Changing the base of numbers is simplified. • Scientific and graphing calculators provide logarithm functions for base ...
... • Multiplication and division are reduced to simple addition and subtraction. • Exponentiation and root operations are reduced to more simple exponent multiplication or division. • Changing the base of numbers is simplified. • Scientific and graphing calculators provide logarithm functions for base ...
24(4)
... issue as a whole and, except where otherwise noted, rights to each individual contribution. ...
... issue as a whole and, except where otherwise noted, rights to each individual contribution. ...