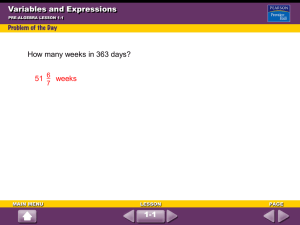
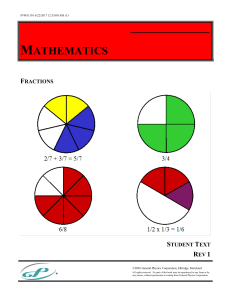
Standard Grade - Maths4Scotland
... To get rid the surd – multiply top and bottom by the conjugate conjugate - the same expression with the opposite sign in the middle ...
... To get rid the surd – multiply top and bottom by the conjugate conjugate - the same expression with the opposite sign in the middle ...
Lecture 8 - WordPress.com
... Normally cocktail sort or shaker sort pass (one time in both directions) is counted as two bubble sort passes. In a typical implementation the cocktail sort is less than two times faster than a bubble sort implementation. Because you have to implement a loop in both directions that is changing ...
... Normally cocktail sort or shaker sort pass (one time in both directions) is counted as two bubble sort passes. In a typical implementation the cocktail sort is less than two times faster than a bubble sort implementation. Because you have to implement a loop in both directions that is changing ...
recursion
... Suppose the number of primes is finite, k. The primes are P1, P2….. Pk The largest prime is Pk Consider the number N = 1 + P1, P2….. Pk N is larger than Pk Thus N is not prime. So N must be product of some primes. ...
... Suppose the number of primes is finite, k. The primes are P1, P2….. Pk The largest prime is Pk Consider the number N = 1 + P1, P2….. Pk N is larger than Pk Thus N is not prime. So N must be product of some primes. ...
Introduction to Discrete Mathematics
... US Postal Money Order a11 = a1 + a2 + a3 + … + a8 + a9 + a10 (mod 9) Can it be used to detect transposition error? Correct number ...
... US Postal Money Order a11 = a1 + a2 + a3 + … + a8 + a9 + a10 (mod 9) Can it be used to detect transposition error? Correct number ...