Powers and Roots2
... roots have a special rule when the index is the same as the power the radicand is raised to. Since the n-th root (n is any real number) can be any number, a rule for each number would be not only cumbersome, but impossible since numbers go on forever! Because of that slight problem, the n-th Root Th ...
... roots have a special rule when the index is the same as the power the radicand is raised to. Since the n-th root (n is any real number) can be any number, a rule for each number would be not only cumbersome, but impossible since numbers go on forever! Because of that slight problem, the n-th Root Th ...
Counting Positive and Negative Input Values
... The basics of writing a factorial computation program has been discussed in a factorial example of counting DO. ...
... The basics of writing a factorial computation program has been discussed in a factorial example of counting DO. ...
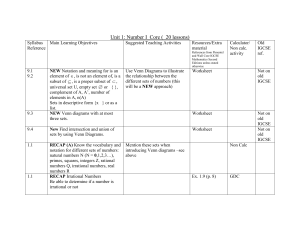
Unit 1 Number I core
... universal set U, empty set or { }, complement of A, A’, number of elements in A, n(A) Sets in descriptive form {x } or as a list. NEW Venn diagrams with at most three sets. ...
... universal set U, empty set or { }, complement of A, A’, number of elements in A, n(A) Sets in descriptive form {x } or as a list. NEW Venn diagrams with at most three sets. ...
7.2
... When multiplying exponential expressions with the same base, add the exponents. Use this sum as the exponent of the common base. When dividing exponential expressions with the same base, subtract the exponents. Use this difference as the exponent of the common base. ...
... When multiplying exponential expressions with the same base, add the exponents. Use this sum as the exponent of the common base. When dividing exponential expressions with the same base, subtract the exponents. Use this difference as the exponent of the common base. ...