Multiplication and Division of Rational Numbers
... a. In the space below, create a word problem that involves integer multiplication. Write an equation to model the situation. ...
... a. In the space below, create a word problem that involves integer multiplication. Write an equation to model the situation. ...
lecture notes 5
... In order to count the elements of a certain set, we replace them with those of another set that has the same number of elements and whose elements are more easily counted. Let A and B be finite sets, and let f be an injective function from A to B. Then there are at least as many elements in B as in ...
... In order to count the elements of a certain set, we replace them with those of another set that has the same number of elements and whose elements are more easily counted. Let A and B be finite sets, and let f be an injective function from A to B. Then there are at least as many elements in B as in ...
recurring decimals vedic style
... labour the whole period of any fraction whose decimal form recurs ! Pupils are, to say the least, intrigued to find that these periods, when longer than their calculator displays, marry up with the front part which the calculator does give them. Anything which promotes the awakening of curiosity des ...
... labour the whole period of any fraction whose decimal form recurs ! Pupils are, to say the least, intrigued to find that these periods, when longer than their calculator displays, marry up with the front part which the calculator does give them. Anything which promotes the awakening of curiosity des ...
February 7 Homework Solutions
... When we find the difference, the only number that is any different is the one in red so we get… |x – y| = x = 0.0000010000000000000000000000000000 ; which has a value base ten of 1/64. If we wanted the value to be less than 1/64, we would do the same thing but just move one place to the right and ma ...
... When we find the difference, the only number that is any different is the one in red so we get… |x – y| = x = 0.0000010000000000000000000000000000 ; which has a value base ten of 1/64. If we wanted the value to be less than 1/64, we would do the same thing but just move one place to the right and ma ...
Exponential Notation
... Sum – The total when adding 2 or more numbers together. Addends – The numbers that are added together. Additive identity –The sum of zero and any number is that number. Example: 7 0 7 Associative law of addition –Changing the grouping of addends does not change their sum. Example: 3 5 ...
... Sum – The total when adding 2 or more numbers together. Addends – The numbers that are added together. Additive identity –The sum of zero and any number is that number. Example: 7 0 7 Associative law of addition –Changing the grouping of addends does not change their sum. Example: 3 5 ...
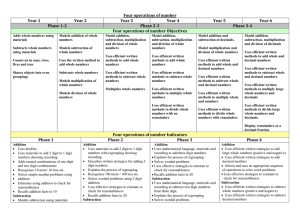
four operations number progression rubric
... Uses materials to subtract 2 digit Uses materials to subtract 2 digit numbers with regrouping showing recording Describes written strategies for subtracting 2 digit numbers Explains basic subtraction facts connecting to addition Recalls subtraction facts to 20 Multiplication Explains wha ...
... Uses materials to subtract 2 digit Uses materials to subtract 2 digit numbers with regrouping showing recording Describes written strategies for subtracting 2 digit numbers Explains basic subtraction facts connecting to addition Recalls subtraction facts to 20 Multiplication Explains wha ...
Teaching Place-Value Concepts: Considerations for Instruction
... Word form: Writing a number using words ...
... Word form: Writing a number using words ...
Powers and Exponents - Simpson County Schools
... real-world to represent extremely large and small numbers. They are also used in solving problems. ...
... real-world to represent extremely large and small numbers. They are also used in solving problems. ...
Elementary arithmetic
Elementary arithmetic is the simplified portion of arithmetic that includes the operations of addition, subtraction, multiplication, and division. It should not be confused with elementary function arithmetic.Elementary arithmetic starts with the natural numbers and the written symbols (digits) that represent them. The process for combining a pair of these numbers with the four basic operations traditionally relies on memorized results for small values of numbers, including the contents of a multiplication table to assist with multiplication and division.Elementary arithmetic also includes fractions and negative numbers, which can be represented on a number line.