How do you compute the midpoint of an interval?
... ∀(ρ1 , ρ2 ) ∈ R2 : ρ1 6 ρ2 =⇒ flhρ1 i 6 flhρ2 i for the same instantiation of flhi in both occurrences. The IEEE 754 standard also mandates that real constants and the result of some operations (addition, subtraction, multiplication, and division, among others) be correctly rounded : ...
... ∀(ρ1 , ρ2 ) ∈ R2 : ρ1 6 ρ2 =⇒ flhρ1 i 6 flhρ2 i for the same instantiation of flhi in both occurrences. The IEEE 754 standard also mandates that real constants and the result of some operations (addition, subtraction, multiplication, and division, among others) be correctly rounded : ...
THE INFINITE CALCULUS
... Each n-periodic nc.system contains n nominal nc. as the first members of their non –negantive whole numerical set and the rest of the set is made of nc. that are derived in shape(deduced) from the n nominal numericals. For example the decimal nc. is made of 10 nominal nc. (0,1,2,3,4,5,6,7,8,9),the r ...
... Each n-periodic nc.system contains n nominal nc. as the first members of their non –negantive whole numerical set and the rest of the set is made of nc. that are derived in shape(deduced) from the n nominal numericals. For example the decimal nc. is made of 10 nominal nc. (0,1,2,3,4,5,6,7,8,9),the r ...
Unit 2: Numbers and Integers - Talent Development Secondary
... statements such as, “It’s like counting with your fingers,” “When cultures didn’t record temperature measurements or numbers representing debt, people didn’t need negative numbers,” or “It’s just like we learned when growing up – start simple.” As a class discuss Exercise 1 and talk about the fact t ...
... statements such as, “It’s like counting with your fingers,” “When cultures didn’t record temperature measurements or numbers representing debt, people didn’t need negative numbers,” or “It’s just like we learned when growing up – start simple.” As a class discuss Exercise 1 and talk about the fact t ...
Chapter #2 Lecture Notes
... o The 4 is in the denominator. A proper fraction is less than one. That means the numerator is less than the denominator. For example, ¾ is a proper fraction because it is < 1. A mixed number is a number that is greater than 1 that has a whole number part and a fractional part. For example, 1¾ i ...
... o The 4 is in the denominator. A proper fraction is less than one. That means the numerator is less than the denominator. For example, ¾ is a proper fraction because it is < 1. A mixed number is a number that is greater than 1 that has a whole number part and a fractional part. For example, 1¾ i ...
Chapter 2 - Data Representation
... • Using only two digits of precision for signed base 10 numbers, the range (interval between lowest and highest numbers) is [-99, +99] and the precision (distance between successive numbers) is 1. • The maximum error, which is the difference between the value of a real number and the closest represe ...
... • Using only two digits of precision for signed base 10 numbers, the range (interval between lowest and highest numbers) is [-99, +99] and the precision (distance between successive numbers) is 1. • The maximum error, which is the difference between the value of a real number and the closest represe ...
IOSR Journal of Mathematics (IOSR-JM)
... Divisibilty of Selected Primes and the Number Generator Method X+ [X./10.^(n-2)]*(5-10.^2)*5.^(0.5*n-2) +[X./10.^(n-4)]*(5-10.^2)*5.^(0.5*n3)+………………………………………………………[X./10.^4]*(5-10.^2)*5 + [X./10.^2]*(5-10.^2); Decomposing 95=19*5 & substituting in the above expansion X-95*([x./10.^(n-2)]+[X./10.^(n ...
... Divisibilty of Selected Primes and the Number Generator Method X+ [X./10.^(n-2)]*(5-10.^2)*5.^(0.5*n-2) +[X./10.^(n-4)]*(5-10.^2)*5.^(0.5*n3)+………………………………………………………[X./10.^4]*(5-10.^2)*5 + [X./10.^2]*(5-10.^2); Decomposing 95=19*5 & substituting in the above expansion X-95*([x./10.^(n-2)]+[X./10.^(n ...
factors - WordPress.com
... 5. 6 is a factor of a number that has 2 and 3 as its factors. We check if the number is even, and also if it is divisible by 3. The number 654 is even It is also divisible by 3 6 is a factor of 654 The number 453 is not even 6 is not a factor of 453 The number 772 is even It is not divisible by 3 6 ...
... 5. 6 is a factor of a number that has 2 and 3 as its factors. We check if the number is even, and also if it is divisible by 3. The number 654 is even It is also divisible by 3 6 is a factor of 654 The number 453 is not even 6 is not a factor of 453 The number 772 is even It is not divisible by 3 6 ...
document
... representatives of numbers. Strictly speaking they are called “numerals”. ° Numbers really have an infinite number of digits • with almost all being same (00…0 or 11…1) except for a few of the rightmost digits • Just don’t normally show leading digits ...
... representatives of numbers. Strictly speaking they are called “numerals”. ° Numbers really have an infinite number of digits • with almost all being same (00…0 or 11…1) except for a few of the rightmost digits • Just don’t normally show leading digits ...
Mathematics - Triumph Learning
... collected 24 oranges and 36 apples. The teacher wants the same number of oranges in every basket. The teacher also wants the same number of apples in every basket. What is the greatest number of baskets the class can make? Step 1: Determine whether you will use common multiples or common factors to ...
... collected 24 oranges and 36 apples. The teacher wants the same number of oranges in every basket. The teacher also wants the same number of apples in every basket. What is the greatest number of baskets the class can make? Step 1: Determine whether you will use common multiples or common factors to ...
Printable Activities
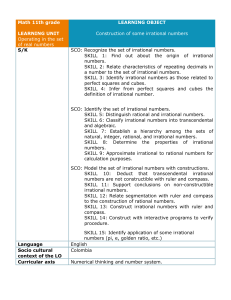
... Learning activity 1) Find out who Hippasus of Metapontum was and his relationship with the origin of irrational numbers. 2) An irrational number is one that: a. Has finite digital digits. b. Is periodic. c. Has infinite decimal digits but no repeating decimal. d. Is on the same straight line. 3) No ...
... Learning activity 1) Find out who Hippasus of Metapontum was and his relationship with the origin of irrational numbers. 2) An irrational number is one that: a. Has finite digital digits. b. Is periodic. c. Has infinite decimal digits but no repeating decimal. d. Is on the same straight line. 3) No ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.