Temperature gradients due to adiabatic plasma
... As the ions get accelerated through the diverging section of the magnetic nozzle their density decreases which the electrons must match to maintain quasineutrality. But the electron pressure gradient must continue to balance the electric field which requires the electron temperature to decrease as w ...
... As the ions get accelerated through the diverging section of the magnetic nozzle their density decreases which the electrons must match to maintain quasineutrality. But the electron pressure gradient must continue to balance the electric field which requires the electron temperature to decrease as w ...
manitoba institute for materials
... Photonic and Phononic Interactions with Materials The interaction of photons and phonons with matter allows materials to be probed over a wide range of length and time scales, providing vital information for understanding their basic properties. Phonons are also one of the elementary excitations of ...
... Photonic and Phononic Interactions with Materials The interaction of photons and phonons with matter allows materials to be probed over a wide range of length and time scales, providing vital information for understanding their basic properties. Phonons are also one of the elementary excitations of ...
magnetic field
... AMPERE’S LAW FOR STATIC MAGNETIC FIELDS For any current geometry that produces a magnetic field that does not change in time, ...
... AMPERE’S LAW FOR STATIC MAGNETIC FIELDS For any current geometry that produces a magnetic field that does not change in time, ...
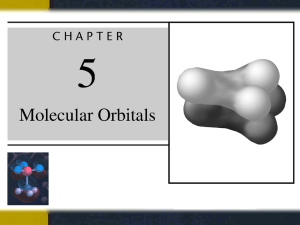
Molecular Orbital Theory
... The orbital motion of electrons creates tiny atomic current loops, which produce magnetic fields. When an external magnetic field is applied to a material, these current loops will tend to align in such a way as to oppose the applied field: induced magnetic fields tend to oppose the change which cre ...
... The orbital motion of electrons creates tiny atomic current loops, which produce magnetic fields. When an external magnetic field is applied to a material, these current loops will tend to align in such a way as to oppose the applied field: induced magnetic fields tend to oppose the change which cre ...
Magnetic Measurements
... reciprocal relationship between electric and magnetic phenomena, which led to his law of induction. He was the first to explain magnetic fields acting at a distance using fictitious lines of force, which eventually led to the concept of field. Following up on Faraday’s work, Heinrich Lenz in 1834 de ...
... reciprocal relationship between electric and magnetic phenomena, which led to his law of induction. He was the first to explain magnetic fields acting at a distance using fictitious lines of force, which eventually led to the concept of field. Following up on Faraday’s work, Heinrich Lenz in 1834 de ...
Magnetic Fields and Magnetic Forces Chapter 27
... Ultimately, Maxwell showed that electricity and magnetism are different manifestations of the same physical laws •“Maxwell’s Equations” for electromagnetism ...
... Ultimately, Maxwell showed that electricity and magnetism are different manifestations of the same physical laws •“Maxwell’s Equations” for electromagnetism ...
Hierarchically Porous Titania Networks with Controllable
... composites is an easy, low cost and scalable process, and is generally recognized as a highly practical approach for fabricating efficient titania photocatalysts for environmental remediation applications. In this study, mixed-phase hierarchically porous titania networks (PTNs) with three-dimensiona ...
... composites is an easy, low cost and scalable process, and is generally recognized as a highly practical approach for fabricating efficient titania photocatalysts for environmental remediation applications. In this study, mixed-phase hierarchically porous titania networks (PTNs) with three-dimensiona ...
Development of magnetic domains in hard ferromagnetic thin films
... Landau–Lifshitz equations for a single crystal of polytwinned domain structure in the reciprocal space using FFT. The three different orientation variants of the L1 0 phase in the polytwinned structure are described by a multicomponent long-range order 共LRO兲 parameter. The coupling of the magnetic d ...
... Landau–Lifshitz equations for a single crystal of polytwinned domain structure in the reciprocal space using FFT. The three different orientation variants of the L1 0 phase in the polytwinned structure are described by a multicomponent long-range order 共LRO兲 parameter. The coupling of the magnetic d ...
Nano-TN 2016 Program
... Recroissance du C60 sur un réseau auto-organisé déposé sur une surface semi-conductrice Self-organization of PS-b-PAA at the air/water interface: a process driven by the release of the solvent spreading Pause café 30 mn Chairman : Nedjma BEN DIAB Electronic Properties of surface and interface In sit ...
... Recroissance du C60 sur un réseau auto-organisé déposé sur une surface semi-conductrice Self-organization of PS-b-PAA at the air/water interface: a process driven by the release of the solvent spreading Pause café 30 mn Chairman : Nedjma BEN DIAB Electronic Properties of surface and interface In sit ...
Potential of Quasicrystals and Quasicrystal Approximants for New
... Al5CuLi3 is a bee lattice of Pauling triacontahedra containing a total of 180 atoms per unit cell. This is actually a small approximant lattice, phases with lattice constants of up to 100 A, containing over 50,000 atoms per unit cell, are known.22 For the best thermoelectric material, Slack suggeste ...
... Al5CuLi3 is a bee lattice of Pauling triacontahedra containing a total of 180 atoms per unit cell. This is actually a small approximant lattice, phases with lattice constants of up to 100 A, containing over 50,000 atoms per unit cell, are known.22 For the best thermoelectric material, Slack suggeste ...
View PDF - CiteSeerX
... only with Sloane’s exposition but with what he learned generally of the Copenhagen point of view. The argument with Sloane . . . had convinced Bell of the central importance of the concept of measurement in any meaningful discussion of quantum mechanics. It was necessary to identify this as a centra ...
... only with Sloane’s exposition but with what he learned generally of the Copenhagen point of view. The argument with Sloane . . . had convinced Bell of the central importance of the concept of measurement in any meaningful discussion of quantum mechanics. It was necessary to identify this as a centra ...
Physical Properties of the NbC Carbide
... The chemical bonding in transition metal carbides is of a complex nature with a covalent, metallic and ionic character. This fact explains the observed physical properties: high hardness and high melting points are properties typical of solids with ionic or covalent bonding, while thermal and electr ...
... The chemical bonding in transition metal carbides is of a complex nature with a covalent, metallic and ionic character. This fact explains the observed physical properties: high hardness and high melting points are properties typical of solids with ionic or covalent bonding, while thermal and electr ...
Section 12: Semiconductors
... rapidly - exponentially - with temperature, particularly by virtue of the exponential factor. Thus as the temperature is raised, a vastly greater number of electrons is excited across the gap. Figure 5 is a plot of log n versus 1/T. The curve is a straight line of slope equal to ( - Eg/2kB). [The T3 ...
... rapidly - exponentially - with temperature, particularly by virtue of the exponential factor. Thus as the temperature is raised, a vastly greater number of electrons is excited across the gap. Figure 5 is a plot of log n versus 1/T. The curve is a straight line of slope equal to ( - Eg/2kB). [The T3 ...
Competition between Superconductivity and Charge Density Waves
... 1.1.4 Type I and Type II superconductors . . . . . . . . . 1.2 The Landau-Ginzburg theory . . . . . . . . . . . . . . . . . . 1.2.1 The Ginzburg-Landau equations . . . . . . . . . . . . 1.2.2 The two characteristic lengths ξ(T ), λ(T ) . . . . . . . 1.2.3 The Ginzburg-Landau parameter κ(T ) . . . . ...
... 1.1.4 Type I and Type II superconductors . . . . . . . . . 1.2 The Landau-Ginzburg theory . . . . . . . . . . . . . . . . . . 1.2.1 The Ginzburg-Landau equations . . . . . . . . . . . . 1.2.2 The two characteristic lengths ξ(T ), λ(T ) . . . . . . . 1.2.3 The Ginzburg-Landau parameter κ(T ) . . . . ...
Condensed matter physics

Condensed matter physics is a branch of physics that deals with the physical properties of condensed phases of matter. Condensed matter physicists seek to understand the behavior of these phases by using physical laws. In particular, these include the laws of quantum mechanics, electromagnetism and statistical mechanics.The most familiar condensed phases are solids and liquids, while more exotic condensed phases include the superconducting phase exhibited by certain materials at low temperature, the ferromagnetic and antiferromagnetic phases of spins on atomic lattices, and the Bose–Einstein condensate found in cold atomic systems. The study of condensed matter physics involves measuring various material properties via experimental probes along with using techniques of theoretical physics to develop mathematical models that help in understanding physical behavior.The diversity of systems and phenomena available for study makes condensed matter physics the most active field of contemporary physics: one third of all American physicists identify themselves as condensed matter physicists, and the Division of Condensed Matter Physics is the largest division at the American Physical Society. The field overlaps with chemistry, materials science, and nanotechnology, and relates closely to atomic physics and biophysics. Theoretical condensed matter physics shares important concepts and techniques with theoretical particle and nuclear physics.A variety of topics in physics such as crystallography, metallurgy, elasticity, magnetism, etc., were treated as distinct areas, until the 1940s when they were grouped together as solid state physics. Around the 1960s, the study of physical properties of liquids was added to this list, forming the basis for the new, related specialty of condensed matter physics. According to physicist Phil Anderson, the term was coined by him and Volker Heine when they changed the name of their group at the Cavendish Laboratories, Cambridge from ""Solid state theory"" to ""Theory of Condensed Matter"" in 1967, as they felt it did not exclude their interests in the study of liquids, nuclear matter and so on. Although Anderson and Heine helped popularize the name ""condensed matter"", it had been present in Europe for some years, most prominently in the form of a journal published in English, French, and German by Springer-Verlag titled Physics of Condensed Matter, which was launched in 1963. The funding environment and Cold War politics of the 1960s and 1970s were also factors that lead some physicists to prefer the name ""condensed matter physics"", which emphasized the commonality of scientific problems encountered by physicists working on solids, liquids, plasmas, and other complex matter, over ""solid state physics"", which was often associated with the industrial applications of metals and semiconductors. The Bell Telephone Laboratories was one of the first institutes to conduct a research program in condensed matter physics.References to ""condensed"" state can be traced to earlier sources. For example, in the introduction to his 1947 ""Kinetic theory of liquids"" book, Yakov Frenkel proposed that ""The kinetic theory of liquids must accordingly be developed as a generalization and extension of the kinetic theory of solid bodies"". As a matter of fact, it would be more correct to unify them under the title of ""condensed bodies"".