Basic Arithmetic - Learning for Knowledge
... Numbers can be classified as Integers, Whole numbers and Natural number sets. These sets of numbers are discrete, meaning each number in a set is more or one less than the next number in the set. Quotients are ratios of any two discrete numbers and are elements of another set. Number sets can be rep ...
... Numbers can be classified as Integers, Whole numbers and Natural number sets. These sets of numbers are discrete, meaning each number in a set is more or one less than the next number in the set. Quotients are ratios of any two discrete numbers and are elements of another set. Number sets can be rep ...
Elliptic Curves and Elliptic Curve Cryptography
... Let a and b be real numbers. An elliptic curve E over the field of real numbers R is the set of points (x,y) with x and y in R that satisfy the equation together with a single element , called the point at infinity. There are other types of elliptic curves, but we’ll only consider elliptic curves o ...
... Let a and b be real numbers. An elliptic curve E over the field of real numbers R is the set of points (x,y) with x and y in R that satisfy the equation together with a single element , called the point at infinity. There are other types of elliptic curves, but we’ll only consider elliptic curves o ...
Vertex Form of Quadratic Equations
... Is there a way to tell how many x-intercepts a parabola will have without solving the equation? Yes, use the discriminant (also called the radicand of the quadratic formula – see page 293 of textbook) ...
... Is there a way to tell how many x-intercepts a parabola will have without solving the equation? Yes, use the discriminant (also called the radicand of the quadratic formula – see page 293 of textbook) ...
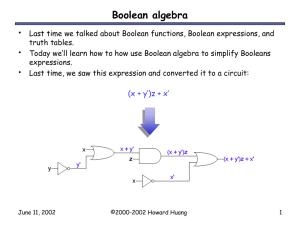
Boolean Algebra
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...