The geometry of orthogonal groups over finite fields
... This lecture note is based on the lectures given at Kyushu University in 1994 and at Ateneo de Manila University in 1995. In these lectures I presented the theory of quadratic forms over finite fields. The emphasis is placed on geometric and combinatorial objects, rather than the orthogonal group it ...
... This lecture note is based on the lectures given at Kyushu University in 1994 and at Ateneo de Manila University in 1995. In these lectures I presented the theory of quadratic forms over finite fields. The emphasis is placed on geometric and combinatorial objects, rather than the orthogonal group it ...
1 Prime numbers
... Let us start with recalling/formalising the principle of division with remainder. Theorem 1.1 (The division algorithm). Let a and b be natural numbers with b 6= 0. There exist unique natural numbers q and r such that a = bq + r and 0 6 r < b. Proof. To show existence, note that if a < b then q = 0 a ...
... Let us start with recalling/formalising the principle of division with remainder. Theorem 1.1 (The division algorithm). Let a and b be natural numbers with b 6= 0. There exist unique natural numbers q and r such that a = bq + r and 0 6 r < b. Proof. To show existence, note that if a < b then q = 0 a ...
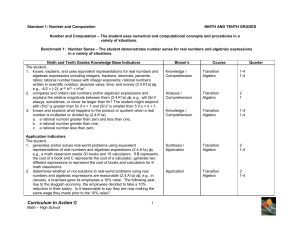
Ninth and Tenth Grades Knowledge Base Indicators
... a. N linear equations and inequalities both analytically and graphically; b. quadratic equations with integer solutions (may be solved by trial and error, graphing, quadratic formula, or factoring); c. ▲N systems of linear equations with two unknowns using integer coefficients and constants; d. radi ...
... a. N linear equations and inequalities both analytically and graphically; b. quadratic equations with integer solutions (may be solved by trial and error, graphing, quadratic formula, or factoring); c. ▲N systems of linear equations with two unknowns using integer coefficients and constants; d. radi ...
Compound propositions
... 1. Give an example of a function that is one-to-one but not onto 2. Give an example of a function that is onto but not one-to-one. 3. Give an example of a function that is neither one-to-one nor onto 4. Give an example of a function that is both one-to-one and onto 5. How many functions are there fr ...
... 1. Give an example of a function that is one-to-one but not onto 2. Give an example of a function that is onto but not one-to-one. 3. Give an example of a function that is neither one-to-one nor onto 4. Give an example of a function that is both one-to-one and onto 5. How many functions are there fr ...
C2 Worksheet A
... When f(x) is divided by (x + 1) there is a remainder of −4. When f(x) is divided by (x − 2) there is a remainder of 80. a Find the values of the constants p and q. b Show that (x + 2) is a factor of f(x). c Solve the equation f(x) = 0. ...
... When f(x) is divided by (x + 1) there is a remainder of −4. When f(x) is divided by (x − 2) there is a remainder of 80. a Find the values of the constants p and q. b Show that (x + 2) is a factor of f(x). c Solve the equation f(x) = 0. ...
Sample pages 2 PDF
... 3. A number N is called multi-perfect if it divides its sum of divisors but is not perfect i.e., σ (N) = kN holds with an integer k ≥ 3. Several such numbers had already been found in the 17th century by Descartes, P. Fermat16 and A. Jumeau (see [1545]), the first few being 120, 672, 30 240, 32 760, ...
... 3. A number N is called multi-perfect if it divides its sum of divisors but is not perfect i.e., σ (N) = kN holds with an integer k ≥ 3. Several such numbers had already been found in the 17th century by Descartes, P. Fermat16 and A. Jumeau (see [1545]), the first few being 120, 672, 30 240, 32 760, ...