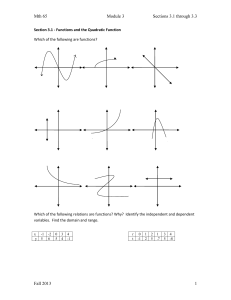
Mth 65 Module 3 Sections 3.1 through 3.3 Section 3.1
... The function above is called a _______________________________function. The shape of the graph is called a ___________________________. Each parabola has a _______________(maximum or minimum) and an axis of symmetry (always a ______________________ line which passes through the vertex). State the ve ...
... The function above is called a _______________________________function. The shape of the graph is called a ___________________________. Each parabola has a _______________(maximum or minimum) and an axis of symmetry (always a ______________________ line which passes through the vertex). State the ve ...
Real Numbers - Abstractmath.org
... I will not give a mathematical definition of “real number”. There are several equivalent definitions of real number all of which are quite complicated. Mathematicians rarely think about real numbers in terms of these definitions; what they have in mind when they work with them are their familiar alg ...
... I will not give a mathematical definition of “real number”. There are several equivalent definitions of real number all of which are quite complicated. Mathematicians rarely think about real numbers in terms of these definitions; what they have in mind when they work with them are their familiar alg ...
Mth 65 Module 3 Sections 3.1 through 3.3 Section 3.1
... The function above is called a _______________________________function. The shape of the graph is called a ___________________________. Each parabola has a _______________(maximum or minimum) and an axis of symmetry (always a ______________________ line which passes through the vertex). State the ve ...
... The function above is called a _______________________________function. The shape of the graph is called a ___________________________. Each parabola has a _______________(maximum or minimum) and an axis of symmetry (always a ______________________ line which passes through the vertex). State the ve ...
Default Normal Template
... 2x 5 21 implies that 2x – 5 = 21 or 2x – 5 = - 21. Solving these equations ...
... 2x 5 21 implies that 2x – 5 = 21 or 2x – 5 = - 21. Solving these equations ...
22 - AbstractAlgebra.net: The home of introductory abstract algebra
... Let G be any group. We will show that G can be viewed as a group of permutations acting on its own elements. For any g ∈ G, let Tg denote the function Tg : G → G via x 7→ xg, that is, Tg is right multiplication by g. Note: Gallian uses left multiplication Tg since he composes group operations from r ...
... Let G be any group. We will show that G can be viewed as a group of permutations acting on its own elements. For any g ∈ G, let Tg denote the function Tg : G → G via x 7→ xg, that is, Tg is right multiplication by g. Note: Gallian uses left multiplication Tg since he composes group operations from r ...
2005 Mississippi Mu Alpha Theta Inter-School Test
... 1. Let x, y, and z be three prime numbers such that x + y = z. If 1 < x < y, find x. 2. In a certain school, the ratio of girls to boys is 9 to 8. If the girls’ average age is 12 and the boys’ average age is 11, find the average age of all children in the school. 3. Let a = xy, b = xz, and c = yz su ...
... 1. Let x, y, and z be three prime numbers such that x + y = z. If 1 < x < y, find x. 2. In a certain school, the ratio of girls to boys is 9 to 8. If the girls’ average age is 12 and the boys’ average age is 11, find the average age of all children in the school. 3. Let a = xy, b = xz, and c = yz su ...






![[hal-00137158, v1] Well known theorems on triangular systems and](http://s1.studyres.com/store/data/015177460_1-823a690e284005713c70fc9e95ccaaf8-300x300.png)
















