on end0m0rpb3sms of abelian topological groups
... (ii) X generates F(X) algebraically, and (hi) for every continuous map tpoiX into any topological group G such that
... (ii) X generates F(X) algebraically, and (hi) for every continuous map tpoiX into any topological group G such that
Module 1 Structure o..
... With this module, we begin the study of numbers. Some of the information will be quite familiar and some will be new. I hope you enjoy the new material and that it informs your intuition and knowledge of numbers for years to come. We start with the most basic structure in math: sets. A set is a col ...
... With this module, we begin the study of numbers. Some of the information will be quite familiar and some will be new. I hope you enjoy the new material and that it informs your intuition and knowledge of numbers for years to come. We start with the most basic structure in math: sets. A set is a col ...
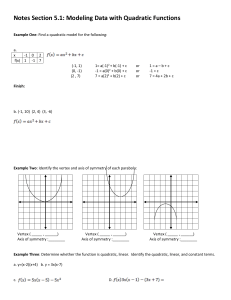
Notes Section 5.1: Modeling Data with Quadratic Functions Example
... A player throws a ball up and toward a wall that is 17 feet high. The height h in feet of the ball t seconds after it leaves the player’s hand is modeled by h = -16t2+25t+6. If the ball makes it to where the wall is, will it go over the wall or hit the wall? h = -16t2+25t+6 17= -16t2+25t+6 ...
... A player throws a ball up and toward a wall that is 17 feet high. The height h in feet of the ball t seconds after it leaves the player’s hand is modeled by h = -16t2+25t+6. If the ball makes it to where the wall is, will it go over the wall or hit the wall? h = -16t2+25t+6 17= -16t2+25t+6 ...