Solve an “And” Compound Inequality
... B. Solve 3 < |d|. Graph the solution set on a number line. 3 < |d| means that the distance between d and 0 on a number line is greater than 3 units. To make 3 < |d| true, you must substitute values for d that are greater than 3 units from 0. Notice that the graph of 3 < |d| is the same as the graph ...
... B. Solve 3 < |d|. Graph the solution set on a number line. 3 < |d| means that the distance between d and 0 on a number line is greater than 3 units. To make 3 < |d| true, you must substitute values for d that are greater than 3 units from 0. Notice that the graph of 3 < |d| is the same as the graph ...
4.1 The Graph of a Linear Equation
... Two distinct lines in the plane either are parallel or they intersect. In exercises 55 to 58, graph each pair of equations on the same set of axes, and find the point of intersection, ...
... Two distinct lines in the plane either are parallel or they intersect. In exercises 55 to 58, graph each pair of equations on the same set of axes, and find the point of intersection, ...
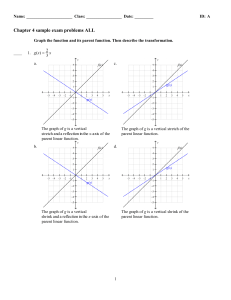
Identify the type of function represented by each graph. 2 - MOC-FV
... Coefficients greater than 1 cause the graph to be stretched vertically and coefficients between 0 and 1 cause the graph to be compressed vertically. The variable x in the parent function y = x is multiplied by 3. So, the graph will be stretched vertically. ...
... Coefficients greater than 1 cause the graph to be stretched vertically and coefficients between 0 and 1 cause the graph to be compressed vertically. The variable x in the parent function y = x is multiplied by 3. So, the graph will be stretched vertically. ...
Functions: The domain and range Jackie Nicholas Jacquie
... The definition we have given is a general one. While in the examples we have used numbers as elements of X and Y , there is no reason why this must be so. However, in these notes we will only consider functions where X and Y are subsets of the real numbers. In this setting, we often describe a functi ...
... The definition we have given is a general one. While in the examples we have used numbers as elements of X and Y , there is no reason why this must be so. However, in these notes we will only consider functions where X and Y are subsets of the real numbers. In this setting, we often describe a functi ...
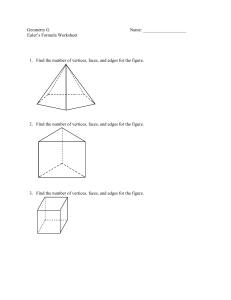
Dual graph
In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge whenever two faces of G are separated from each other by an edge. Thus, each edge e of G has a corresponding dual edge, the edge that connects the two faces on either side of e.Graph duality is a topological generalization of the geometric concepts of dual polyhedra and dual tessellations, and is in turn generalized algebraically by the concept of a dual matroid. Variations of planar graph duality include a version of duality for directed graphs, and duality for graphs embedded onto non-planar two-dimensional surfaces.However, the notion described in this page is different from the edge-to-vertex dual (line graph) of a graph and should not be confused with it.The term ""dual"" is used because this property is symmetric, meaning that if H is a dual of G, then G is a dual of H (if G is connected). When discussing the dual of a graph G, the graph G itself may be referred to as the ""primal graph"". Many other graph properties and structures may be translated into other natural properties and structures of the dual. For instance, cycles are dual to cuts, spanning trees are dual to the complements of spanning trees, and simple graphs (without parallel edges or self-loops) are dual to 3-edge-connected graphs.Polyhedral graphs, and some other planar graphs, have unique dual graphs. However, for planar graphs more generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph. Testing whether one planar graph is dual to another is NP-complete.