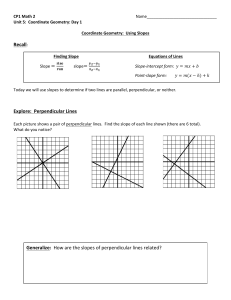
Graph each ordered pair on a coordinate plane. 2. A(2, 5
... b. Graph Graph the ordered pairs. c. Words Describe the shape of the graph. d. Words If possible, write a rule to find the twentieth term. Explain how you found the rule or why you cannot write a rule. SOLUTION: a. The set of ordered pairs is {(1, 4), (2, 7), (3, 10), (4, 13)}. b. ...
... b. Graph Graph the ordered pairs. c. Words Describe the shape of the graph. d. Words If possible, write a rule to find the twentieth term. Explain how you found the rule or why you cannot write a rule. SOLUTION: a. The set of ordered pairs is {(1, 4), (2, 7), (3, 10), (4, 13)}. b. ...
Discrete Mathematics
... defined dually as an element of P which is less than or equal to every element of S. A set with an upper bound is said to be bounded from above by that bound, a set with a lower bound is said to be bounded from below by that bound. ...
... defined dually as an element of P which is less than or equal to every element of S. A set with an upper bound is said to be bounded from above by that bound, a set with a lower bound is said to be bounded from below by that bound. ...
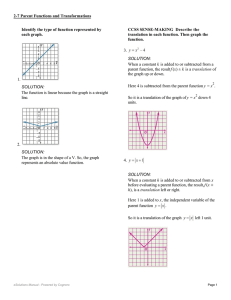
Identify the type of function represented by each graph. 1
... eSolutions Manual - Powered by Cognero h), is a translation left or right. When a constant k is added to or subtracted from a parent function, the result f (x) ± k is a translation of ...
... eSolutions Manual - Powered by Cognero h), is a translation left or right. When a constant k is added to or subtracted from a parent function, the result f (x) ± k is a translation of ...
Dual graph
In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge whenever two faces of G are separated from each other by an edge. Thus, each edge e of G has a corresponding dual edge, the edge that connects the two faces on either side of e.Graph duality is a topological generalization of the geometric concepts of dual polyhedra and dual tessellations, and is in turn generalized algebraically by the concept of a dual matroid. Variations of planar graph duality include a version of duality for directed graphs, and duality for graphs embedded onto non-planar two-dimensional surfaces.However, the notion described in this page is different from the edge-to-vertex dual (line graph) of a graph and should not be confused with it.The term ""dual"" is used because this property is symmetric, meaning that if H is a dual of G, then G is a dual of H (if G is connected). When discussing the dual of a graph G, the graph G itself may be referred to as the ""primal graph"". Many other graph properties and structures may be translated into other natural properties and structures of the dual. For instance, cycles are dual to cuts, spanning trees are dual to the complements of spanning trees, and simple graphs (without parallel edges or self-loops) are dual to 3-edge-connected graphs.Polyhedral graphs, and some other planar graphs, have unique dual graphs. However, for planar graphs more generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph. Testing whether one planar graph is dual to another is NP-complete.