Lecture Materials
... Around 300 BC, Euclid gave the definitions of points and lines that withstood two millennia of diligent study. The mathematicians of the 19thfound them lacking. According to Euclid, A point is that which has no part. As F. Klein [Klein, p. 196] notes "a point is by no means determined by this proper ...
... Around 300 BC, Euclid gave the definitions of points and lines that withstood two millennia of diligent study. The mathematicians of the 19thfound them lacking. According to Euclid, A point is that which has no part. As F. Klein [Klein, p. 196] notes "a point is by no means determined by this proper ...
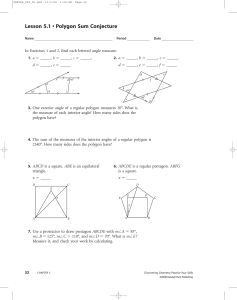
Practice Your Skills for Chapter 5
... 8. _____ Opposite sides are congruent. 10. _____ Both diagonals bisect angles. ...
... 8. _____ Opposite sides are congruent. 10. _____ Both diagonals bisect angles. ...
Lecture (11) - MIT OpenCourseWare
... Proof. If X is a disjoint union of open sets U and V , then we can construct an idempotent e ⊂= 0, 1 by taking the pullback of 0 along U � Spec Z and the pullback of 1 along V � Spec Z. Conversely, if e ∩ �(X, OX ) is an idempotent, then its value at each x ∩ X is either 0 or 1; the sets where the t ...
... Proof. If X is a disjoint union of open sets U and V , then we can construct an idempotent e ⊂= 0, 1 by taking the pullback of 0 along U � Spec Z and the pullback of 1 along V � Spec Z. Conversely, if e ∩ �(X, OX ) is an idempotent, then its value at each x ∩ X is either 0 or 1; the sets where the t ...
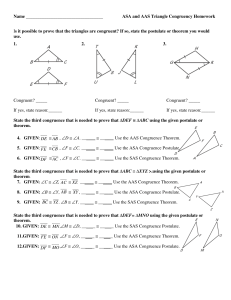
ASA and AAS Triangle Congruency Homework Is it possible
... State the third congruence that is needed to prove that ∆DEF ≅ ∆ABC using the given postulate or theorem. 4. GIVEN: DE ≅ AB , ∠D ≅ ∠A. ______ ≅ ______ Use the AAS Congruence Theorem. 5. GIVEN: FE ≅ CB , ∠F ≅ ∠C. ______ ≅ ______ Use the ASA Congruence Postulate. 6. GIVEN: DF ≅ AC , ∠F ≅ ∠C. ______ ≅ ...
... State the third congruence that is needed to prove that ∆DEF ≅ ∆ABC using the given postulate or theorem. 4. GIVEN: DE ≅ AB , ∠D ≅ ∠A. ______ ≅ ______ Use the AAS Congruence Theorem. 5. GIVEN: FE ≅ CB , ∠F ≅ ∠C. ______ ≅ ______ Use the ASA Congruence Postulate. 6. GIVEN: DF ≅ AC , ∠F ≅ ∠C. ______ ≅ ...
3-manifold

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. Intuitively, a 3-manifold can be thought of as a possible shape of the universe. Just like a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
















![THE HIGHER HOMOTOPY GROUPS 1. Definitions Let I = [0,1] be](http://s1.studyres.com/store/data/001160219_1-57248e6267c8b98f385fc9eb1b30c0a7-300x300.png)