Non-Euclidean Geometry
... Start with 2 equal line segments AC and BD perpendicular to a line AB. Join CD. It is easy to show that ! C = ! D. Saccheri then considered three cases: (1) ! C = ! D = a right angle. (2) ! C = ! D > a right angle. (3) ! C = ! D < a right angle. The first case is the Euclidean case. He wished to sho ...
... Start with 2 equal line segments AC and BD perpendicular to a line AB. Join CD. It is easy to show that ! C = ! D. Saccheri then considered three cases: (1) ! C = ! D = a right angle. (2) ! C = ! D > a right angle. (3) ! C = ! D < a right angle. The first case is the Euclidean case. He wished to sho ...
Postulates and Theorems, Geometry Honors
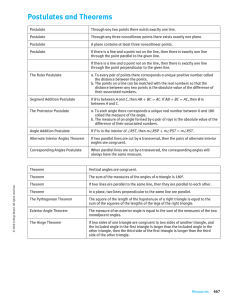
... a. To every pair of points there corresponds a unique positive number called the distance between the points. b. The points on a line can be matched with the real numbers so that the distance between any two points is the absolute value of the difference of their associated numbers. ...
... a. To every pair of points there corresponds a unique positive number called the distance between the points. b. The points on a line can be matched with the real numbers so that the distance between any two points is the absolute value of the difference of their associated numbers. ...
Topology Proceedings - topo.auburn.edu
... serve BCG. It follows from the second part of Claim 3 and the description of the map f of Example 2 that f cannot be blended. The two reasons for non-blendedness of f given so far rely heavily on the fact that f is compact. Let us conclude this note with an argument that does not rely on compactness ...
... serve BCG. It follows from the second part of Claim 3 and the description of the map f of Example 2 that f cannot be blended. The two reasons for non-blendedness of f given so far rely heavily on the fact that f is compact. Let us conclude this note with an argument that does not rely on compactness ...
fragmentability by the discrete metric
... Proof. Clearly, (iii) ⇒ (ii) and so by Theorem 6 it is sufficient to show that (ii) ⇒ (iii). Suppose that Z is a complete metric space and f : Z → (X, τ) is quasi-continuous. Since (X, τ) is metrisable, we have from [1] that there exists a dense Gδ subset G of Z such that f is continuous at each poi ...
... Proof. Clearly, (iii) ⇒ (ii) and so by Theorem 6 it is sufficient to show that (ii) ⇒ (iii). Suppose that Z is a complete metric space and f : Z → (X, τ) is quasi-continuous. Since (X, τ) is metrisable, we have from [1] that there exists a dense Gδ subset G of Z such that f is continuous at each poi ...
3-manifold

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. Intuitively, a 3-manifold can be thought of as a possible shape of the universe. Just like a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.