Introduction to Momentum
... A golf ball with mass 5.0 x 10-2 kg is struck with a club. The force on the ball varies from zero when contact is made up to some maximum value (when the ball is maximally deformed) and then back to zero when the ball leaves the club. Assume that the ball leaves the club face with a velocity of 44 m ...
... A golf ball with mass 5.0 x 10-2 kg is struck with a club. The force on the ball varies from zero when contact is made up to some maximum value (when the ball is maximally deformed) and then back to zero when the ball leaves the club. Assume that the ball leaves the club face with a velocity of 44 m ...
PPT_W07D1_mac
... Impulse Demo To explain the demo and the example we need concepts of momentum and impulse An explanation is easier if we also use the idea of center of mass ...
... Impulse Demo To explain the demo and the example we need concepts of momentum and impulse An explanation is easier if we also use the idea of center of mass ...
Phy 211: General Physics I
... A specific type of interaction between 2 objects. The basic assumptions of a collision: 1. Interaction is short lived compared to the time of observation 2. A relatively large force acts on each colliding object 3. The motion of one or both objects changes abruptly following ...
... A specific type of interaction between 2 objects. The basic assumptions of a collision: 1. Interaction is short lived compared to the time of observation 2. A relatively large force acts on each colliding object 3. The motion of one or both objects changes abruptly following ...
Momentum
... orange and the other yellow, are involved in a perfectly elastic glancing collision. The yellow disk is initially at rest and is struck by the orange disk moving with a speed of 5 m/s. After the collision, the orange disk moves along a direction that makes an angle of 37 with its initial direction ...
... orange and the other yellow, are involved in a perfectly elastic glancing collision. The yellow disk is initially at rest and is struck by the orange disk moving with a speed of 5 m/s. After the collision, the orange disk moves along a direction that makes an angle of 37 with its initial direction ...
Phy 211: General Physics I
... The total linear momentum of a system will remain constant when no external net force acts upon the system, or (p1 + p2 + ...)before collision= (p1 + p2 + ...)after collision • Note: Individual momentum vectors may change due to collisions, etc. but the linear momentum for the system remains constan ...
... The total linear momentum of a system will remain constant when no external net force acts upon the system, or (p1 + p2 + ...)before collision= (p1 + p2 + ...)after collision • Note: Individual momentum vectors may change due to collisions, etc. but the linear momentum for the system remains constan ...
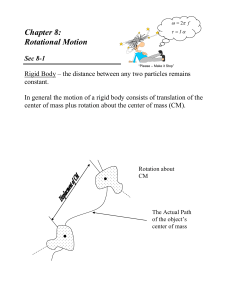
Chapter 15
... motion is caused by gravitational attraction forces. Since these forces act in pairs, the sum of the moments of the forces acting on the system will be zero. This means that angular momentum is conserved. If the angular momentum is constant, does it mean the linear momentum is also constant? Why or ...
... motion is caused by gravitational attraction forces. Since these forces act in pairs, the sum of the moments of the forces acting on the system will be zero. This means that angular momentum is conserved. If the angular momentum is constant, does it mean the linear momentum is also constant? Why or ...
Lecture 8: Forces & The Laws of Motion
... Momentum: Practice Problem A 50-kg girl is standing on a 100-kg plank. The plank, originally at rest, is free to slide on a frozen lake, which is a flat, frictionless surface. The girl begins to walk along the plank at a constant velocity of 2 m/s to the right relative to the plank. -What is her ve ...
... Momentum: Practice Problem A 50-kg girl is standing on a 100-kg plank. The plank, originally at rest, is free to slide on a frozen lake, which is a flat, frictionless surface. The girl begins to walk along the plank at a constant velocity of 2 m/s to the right relative to the plank. -What is her ve ...
VI. Conservation of Energy and Momentum C. Momentum 12. The
... continues on at a velocity of 3.0 m/s what will be the velocity of the pin after the collision? A 5 kg bowling ball is rolling in the gutter towards the pins at 2.4 m/s. A second bowling ball with a mass of 6 kg is thrown in the gutter and rolls at 4.6 m/s. It eventually hits the smaller ball and th ...
... continues on at a velocity of 3.0 m/s what will be the velocity of the pin after the collision? A 5 kg bowling ball is rolling in the gutter towards the pins at 2.4 m/s. A second bowling ball with a mass of 6 kg is thrown in the gutter and rolls at 4.6 m/s. It eventually hits the smaller ball and th ...
Non-sticky collisions
... example, a 0.1 kg baseball moving at 40 m/s has a momentum of 4 kg.m/s in the direction it’s moving. But a 1,200kg car moving at the same speed as the baseball has a much greater momentum: 48,000 kg.m/s. Conservation of momentum: If you are driving a go-cart and crash into another go-car at rest and ...
... example, a 0.1 kg baseball moving at 40 m/s has a momentum of 4 kg.m/s in the direction it’s moving. But a 1,200kg car moving at the same speed as the baseball has a much greater momentum: 48,000 kg.m/s. Conservation of momentum: If you are driving a go-cart and crash into another go-car at rest and ...
2. energy and momentum
... If you fall off something, what sort of surface would you prefer to land on? Explain! ...
... If you fall off something, what sort of surface would you prefer to land on? Explain! ...
7-2 Conservation of Momentum During a collision, measurements
... 7-2 Conservation of Momentum Momentum conservation works for a rocket as long as we consider the rocket and its fuel to be one system, and account for the mass loss of the rocket. ...
... 7-2 Conservation of Momentum Momentum conservation works for a rocket as long as we consider the rocket and its fuel to be one system, and account for the mass loss of the rocket. ...
Relativistic angular momentum
""Angular momentum tensor"" redirects to here.In physics, relativistic angular momentum refers to the mathematical formalisms and physical concepts that define angular momentum in special relativity (SR) and general relativity (GR). The relativistic quantity is subtly different from the three-dimensional quantity in classical mechanics.Angular momentum is a dynamical quantity derived from position and momentum, and is important; angular momentum is a measure of an object's ""amount of rotational motion"" and resistance to stop rotating. Also, in the same way momentum conservation corresponds to translational symmetry, angular momentum conservation corresponds to rotational symmetry – the connection between symmetries and conservation laws is made by Noether's theorem. While these concepts were originally discovered in classical mechanics – they are also true and significant in special and general relativity. In terms of abstract algebra; the invariance of angular momentum, four-momentum, and other symmetries in spacetime, are described by the Poincaré group and Lorentz group.Physical quantities which remain separate in classical physics are naturally combined in SR and GR by enforcing the postulates of relativity, an appealing characteristic. Most notably; space and time coordinates combine into the four-position, and energy and momentum combine into the four-momentum. These four-vectors depend on the frame of reference used, and change under Lorentz transformations to other inertial frames or accelerated frames.Relativistic angular momentum is less obvious. The classical definition of angular momentum is the cross product of position x with momentum p to obtain a pseudovector x×p, or alternatively as the exterior product to obtain a second order antisymmetric tensor x∧p. What does this combine with, if anything? There is another vector quantity not often discussed – it is the time-varying moment of mass (not the moment of inertia) related to the boost of the centre of mass of the system, and this combines with the classical angular momentum to form an antisymmetric tensor of second order. For rotating mass–energy distributions (such as gyroscopes, planets, stars, and black holes) instead of point-like particles, the angular momentum tensor is expressed in terms of the stress–energy tensor of the rotating object.In special relativity alone, in the rest frame of a spinning object; there is an intrinsic angular momentum analogous to the ""spin"" in quantum mechanics and relativistic quantum mechanics, although for an extended body rather than a point particle. In relativistic quantum mechanics, elementary particles have spin and this is an additional contribution to the orbital angular momentum operator, yielding the total angular momentum tensor operator. In any case, the intrinsic ""spin"" addition to the orbital angular momentum of an object can be expressed in terms of the Pauli–Lubanski pseudovector.