Document
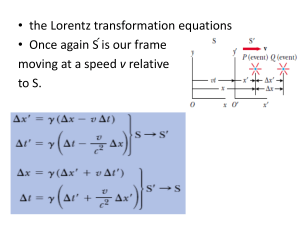
... say that the speed should be the sum of the two speeds, or 1.50c. This answer must be incorrect because it contradicts the assertion that no material object can travel faster than the speed of light. • Let two frames or reference be labelled b and d, and suppose that frame d is moving at velocity vd ...
... say that the speed should be the sum of the two speeds, or 1.50c. This answer must be incorrect because it contradicts the assertion that no material object can travel faster than the speed of light. • Let two frames or reference be labelled b and d, and suppose that frame d is moving at velocity vd ...
ch6 momentum
... Inelastic-Example: A rubber ball collides with a hard surface, kinetic energy is lost because ball is deformed during contact with the surface transforming some of the energy into heat. Elastic-(m1v1i + m2v2i = m1v1f + m2v2f) Example: Billiard balls collide without losing any of their energy. Perfec ...
... Inelastic-Example: A rubber ball collides with a hard surface, kinetic energy is lost because ball is deformed during contact with the surface transforming some of the energy into heat. Elastic-(m1v1i + m2v2i = m1v1f + m2v2f) Example: Billiard balls collide without losing any of their energy. Perfec ...
Potential Energy - McMaster University
... time t during the collision of a 58 g ball with a wall. The initial velocity of the ball is 34 m/s perpendicular to the wall. The ball rebounds directly back with approximately the same speed, also perpendicular to the wall. What is Fmax, the maximum magnitude of the force on the ball from the wall ...
... time t during the collision of a 58 g ball with a wall. The initial velocity of the ball is 34 m/s perpendicular to the wall. The ball rebounds directly back with approximately the same speed, also perpendicular to the wall. What is Fmax, the maximum magnitude of the force on the ball from the wall ...
(8%) Write (a) the mass-balance expression and (b) the charge-balance equation
... g. For a reaction A + B, a plot of 1/[A] versus t is a straight line of slope k and intercept l/[A],. therefore the rate law is ...
... g. For a reaction A + B, a plot of 1/[A] versus t is a straight line of slope k and intercept l/[A],. therefore the rate law is ...
File - Phy 2048-0002
... Two astronauts, each having a mass of 75.0 kg, are connected by a 10.0-m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5.00 m/s. Treating the astronauts as particles, calculate (a) the magnitude of the angular momentum of the system and (b) the rota ...
... Two astronauts, each having a mass of 75.0 kg, are connected by a 10.0-m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5.00 m/s. Treating the astronauts as particles, calculate (a) the magnitude of the angular momentum of the system and (b) the rota ...
Slide 1
... Chapter 10 Problem 39 An electric motor turns a flywheel through a drive belt that joins a pulley on the motor and a pulley that is rigidly attached to the flywheel. The flywheel is a solid disk with a mass of 80.0 kg and a diameter of 1.25 m. It turns on a frictionless axle. Its pulley has much sm ...
... Chapter 10 Problem 39 An electric motor turns a flywheel through a drive belt that joins a pulley on the motor and a pulley that is rigidly attached to the flywheel. The flywheel is a solid disk with a mass of 80.0 kg and a diameter of 1.25 m. It turns on a frictionless axle. Its pulley has much sm ...
q - MACscience
... CD reads from the inside to the outside. They used to read 4.3 mega bytes per second. ► They require a constant linear speed of 1.4ms-1. ► This disc needs to rotate at 500rpm at the start and 200rpm at the finish. ► a) Convert 500rpm to rads-1 ► b) a CD can reach the correct ω in one revolution. Wha ...
... CD reads from the inside to the outside. They used to read 4.3 mega bytes per second. ► They require a constant linear speed of 1.4ms-1. ► This disc needs to rotate at 500rpm at the start and 200rpm at the finish. ► a) Convert 500rpm to rads-1 ► b) a CD can reach the correct ω in one revolution. Wha ...
Chapter 7
... quantities q, w, and a, which describe the rotation of the wheel, through the relations: ...
... quantities q, w, and a, which describe the rotation of the wheel, through the relations: ...
Ch 6 Pretest
... a. Momentum is conserved for a system of objects pushing away from each other. b. Momentum is not conserved for a system of objects in a head-on collision. c. Momentum is conserved when two or more interacting objects push away from each other. d. The total momentum of a system of interacting object ...
... a. Momentum is conserved for a system of objects pushing away from each other. b. Momentum is not conserved for a system of objects in a head-on collision. c. Momentum is conserved when two or more interacting objects push away from each other. d. The total momentum of a system of interacting object ...
Lecture-15-10
... wooden sign shown below. The left end of the sign is held in place by a bolt, the right end is tied to a rope that makes an angle of 20.0° with the horizontal. If the sign is uniform, 3.20 m long, and has a mass of 16.0 kg, what is (a) the tension in the rope, and (b) the horizontal and vertical com ...
... wooden sign shown below. The left end of the sign is held in place by a bolt, the right end is tied to a rope that makes an angle of 20.0° with the horizontal. If the sign is uniform, 3.20 m long, and has a mass of 16.0 kg, what is (a) the tension in the rope, and (b) the horizontal and vertical com ...
University Physics-1 Ch-10 NAME: HOMEWORK CHAPTER 10
... kg. These blocks are allowed to move on a fixed wedge of angle θ = 40.0° as shown in Figure P10.37. The coefficient of kinetic friction is 0.20 for both blocks. Draw free-body diagrams of both blocks and of the pulley. Determine (a) the acceleration of the two blocks and (b) the tensions in the stri ...
... kg. These blocks are allowed to move on a fixed wedge of angle θ = 40.0° as shown in Figure P10.37. The coefficient of kinetic friction is 0.20 for both blocks. Draw free-body diagrams of both blocks and of the pulley. Determine (a) the acceleration of the two blocks and (b) the tensions in the stri ...
Document
... The figure shows a glider of mass m1 that can slide without friction on horizontal air tract. It is attached to an object of mass m2 by a massless string. The pulley has radius R and moment of inertia I about it axis of rotation. When released, the hanging object accelerates downward, the glider acc ...
... The figure shows a glider of mass m1 that can slide without friction on horizontal air tract. It is attached to an object of mass m2 by a massless string. The pulley has radius R and moment of inertia I about it axis of rotation. When released, the hanging object accelerates downward, the glider acc ...
Relativistic angular momentum
""Angular momentum tensor"" redirects to here.In physics, relativistic angular momentum refers to the mathematical formalisms and physical concepts that define angular momentum in special relativity (SR) and general relativity (GR). The relativistic quantity is subtly different from the three-dimensional quantity in classical mechanics.Angular momentum is a dynamical quantity derived from position and momentum, and is important; angular momentum is a measure of an object's ""amount of rotational motion"" and resistance to stop rotating. Also, in the same way momentum conservation corresponds to translational symmetry, angular momentum conservation corresponds to rotational symmetry – the connection between symmetries and conservation laws is made by Noether's theorem. While these concepts were originally discovered in classical mechanics – they are also true and significant in special and general relativity. In terms of abstract algebra; the invariance of angular momentum, four-momentum, and other symmetries in spacetime, are described by the Poincaré group and Lorentz group.Physical quantities which remain separate in classical physics are naturally combined in SR and GR by enforcing the postulates of relativity, an appealing characteristic. Most notably; space and time coordinates combine into the four-position, and energy and momentum combine into the four-momentum. These four-vectors depend on the frame of reference used, and change under Lorentz transformations to other inertial frames or accelerated frames.Relativistic angular momentum is less obvious. The classical definition of angular momentum is the cross product of position x with momentum p to obtain a pseudovector x×p, or alternatively as the exterior product to obtain a second order antisymmetric tensor x∧p. What does this combine with, if anything? There is another vector quantity not often discussed – it is the time-varying moment of mass (not the moment of inertia) related to the boost of the centre of mass of the system, and this combines with the classical angular momentum to form an antisymmetric tensor of second order. For rotating mass–energy distributions (such as gyroscopes, planets, stars, and black holes) instead of point-like particles, the angular momentum tensor is expressed in terms of the stress–energy tensor of the rotating object.In special relativity alone, in the rest frame of a spinning object; there is an intrinsic angular momentum analogous to the ""spin"" in quantum mechanics and relativistic quantum mechanics, although for an extended body rather than a point particle. In relativistic quantum mechanics, elementary particles have spin and this is an additional contribution to the orbital angular momentum operator, yielding the total angular momentum tensor operator. In any case, the intrinsic ""spin"" addition to the orbital angular momentum of an object can be expressed in terms of the Pauli–Lubanski pseudovector.