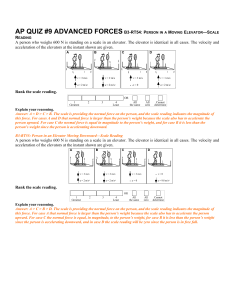
10 Circular Motion
... If you whirl a tin can on the end of a string, you must keep pulling on the string—exerting a centripetal force. The string transmits the centripetal force, pulling the can from a straight-line path into a circular path. ...
... If you whirl a tin can on the end of a string, you must keep pulling on the string—exerting a centripetal force. The string transmits the centripetal force, pulling the can from a straight-line path into a circular path. ...
Physical Science Bell Ringers
... make work easier in two ways, one way is by changing the direction of the applied force, what is the other way? ...
... make work easier in two ways, one way is by changing the direction of the applied force, what is the other way? ...
Ppt
... constant 270 N/m ) on a frictionless surface so that the spring is compressed 0.20 m. When the block is released, it slides across the surface and collides with the 0.60 kg bob of a pendulum. The bob is made of clay and the block sticks to it. The length of the pendulum is 0.80 m. (See the diagram.) ...
... constant 270 N/m ) on a frictionless surface so that the spring is compressed 0.20 m. When the block is released, it slides across the surface and collides with the 0.60 kg bob of a pendulum. The bob is made of clay and the block sticks to it. The length of the pendulum is 0.80 m. (See the diagram.) ...
Document
... constant 270 N/m ) on a frictionless surface so that the spring is compressed 0.20 m. When the block is released, it slides across the surface and collides with the 0.60 kg bob of a pendulum. The bob is made of clay and the block sticks to it. The length of the pendulum is 0.80 m. (See the diagram.) ...
... constant 270 N/m ) on a frictionless surface so that the spring is compressed 0.20 m. When the block is released, it slides across the surface and collides with the 0.60 kg bob of a pendulum. The bob is made of clay and the block sticks to it. The length of the pendulum is 0.80 m. (See the diagram.) ...
Method to calculate electrical forces acting on a sphere in... * Kwangmoo Kim and David Stroud
... ER fluids have potential applications as variable viscosity fluids in automobile devices 关2兴, vibration control 关3兴, and elsewhere. Furthermore, their operating principle is also relevant to other materials, such as magnetorheological 共MR兲 fluids 关4兴. These are suspensions of magnetically permeable ...
... ER fluids have potential applications as variable viscosity fluids in automobile devices 关2兴, vibration control 关3兴, and elsewhere. Furthermore, their operating principle is also relevant to other materials, such as magnetorheological 共MR兲 fluids 关4兴. These are suspensions of magnetically permeable ...
P 2
... the object will float, and the magnitude of the buoyant force is equal to the magnitude of its weight (object < fluid). • If the weight of the object is the same as the weight of the fluid displaced, then the object will neither sink or float (object = fluid). • If the weight of the object is gr ...
... the object will float, and the magnitude of the buoyant force is equal to the magnitude of its weight (object < fluid). • If the weight of the object is the same as the weight of the fluid displaced, then the object will neither sink or float (object = fluid). • If the weight of the object is gr ...
Stress, Strain, Virtual Power and Conservation Principles
... nine numbers are the stresses τij where the subscript i indicates the plane on which the force acts and the subscript j denotes the direction of action. If i = j one has normal stresses and if i 6= j one has shearing stresses. With the above, the stress vector components are expressed as Ti = νj τji ...
... nine numbers are the stresses τij where the subscript i indicates the plane on which the force acts and the subscript j denotes the direction of action. If i = j one has normal stresses and if i 6= j one has shearing stresses. With the above, the stress vector components are expressed as Ti = νj τji ...
Ehrenfest theorem, Galilean invariance and nonlinear Schr\" odinger
... equations with nonlinearities such as that of eq.(9) obey the Ehrenfest relations. Perhaps this is expected as the nonlinear terms are essentially classical, depending on the density ρ and not on the wave function itself. If the external interaction is itself nonlinear such as U(ρ, x), then the Ehre ...
... equations with nonlinearities such as that of eq.(9) obey the Ehrenfest relations. Perhaps this is expected as the nonlinear terms are essentially classical, depending on the density ρ and not on the wave function itself. If the external interaction is itself nonlinear such as U(ρ, x), then the Ehre ...
Glossary for Chapter 1
... Therefore σxx, σyy, and σzz are normal stresses. The normal force over a surface is the net force from shear stress, given by integrating the shear stress over the surface area. The normal stresses are the diagonal elements of the stress tensor. no-slip condition: The requirement that at the interfa ...
... Therefore σxx, σyy, and σzz are normal stresses. The normal force over a surface is the net force from shear stress, given by integrating the shear stress over the surface area. The normal stresses are the diagonal elements of the stress tensor. no-slip condition: The requirement that at the interfa ...
Friction
... • Static friction will oppose a force until such time as the object “breaks away” from the surface with which it is in contact. • The force that is opposed is that component of an applied force that is parallel to the surface of contact. ...
... • Static friction will oppose a force until such time as the object “breaks away” from the surface with which it is in contact. • The force that is opposed is that component of an applied force that is parallel to the surface of contact. ...
Physics Pre AP –Scope and Sequence –Year at a Glance
... Students should understand Newton’s Laws of Motion so that they can give examples of their application. Students should understand how Newton's Second law, F = ma, applies to a body subject to forces such as gravity, the pull of strings, or contact forces so they can: • Draw a well-labeled diagram s ...
... Students should understand Newton’s Laws of Motion so that they can give examples of their application. Students should understand how Newton's Second law, F = ma, applies to a body subject to forces such as gravity, the pull of strings, or contact forces so they can: • Draw a well-labeled diagram s ...
Experiment 7 Simple Harmonic Motion Reading:
... Hooke’s law states that the force resisting the extension of the spring is proportional to the deviation of the spring from its equilibrium position. That is, F = - k x, where x = 0 is defined by the equilibrium position of the spring. If we gently add a mass to the spring, the spring will stretch t ...
... Hooke’s law states that the force resisting the extension of the spring is proportional to the deviation of the spring from its equilibrium position. That is, F = - k x, where x = 0 is defined by the equilibrium position of the spring. If we gently add a mass to the spring, the spring will stretch t ...
What is a wave
... The body of a 1275 kg car is supported on a frame by four springs. Two people riding in the car have a combined mass of 153 kg. When driven over a pothole in the road, the frame vibrates with a period of 0.840 s. For the first few seconds, the vibration approximates simple harmonic motion. Find the ...
... The body of a 1275 kg car is supported on a frame by four springs. Two people riding in the car have a combined mass of 153 kg. When driven over a pothole in the road, the frame vibrates with a period of 0.840 s. For the first few seconds, the vibration approximates simple harmonic motion. Find the ...
Classical central-force problem
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System.