Dynamics – Free Fall, Apparent Weight, and Friction (Honors)
... represent equal magnitude forces acting on the objects the string is attached to. Make sure that you see how that’s represented in Figure 4. The System Newton’s Second Law, ΣF = ma, describes the effect of a net force on an object or group of objects, referred to as the system, that move with some ...
... represent equal magnitude forces acting on the objects the string is attached to. Make sure that you see how that’s represented in Figure 4. The System Newton’s Second Law, ΣF = ma, describes the effect of a net force on an object or group of objects, referred to as the system, that move with some ...
Chapter 6 text
... difference in latitude, the launched rocket lands off course, to the east of Y and appears to have been deflected to the right of its motion. If the rocket were launched from Y to X, it would still appear to veer to the right of its path. We have to consider the Coriolis effect only when dealing wit ...
... difference in latitude, the launched rocket lands off course, to the east of Y and appears to have been deflected to the right of its motion. If the rocket were launched from Y to X, it would still appear to veer to the right of its path. We have to consider the Coriolis effect only when dealing wit ...
AP Physics – Work and Energy
... But what does that mean? Well work is done when something is displaced by a force. If work is done, it takes energy. If you lift a 1 N rock 1 m, you’ve done 1 J of work and expended 1 J of energy. Energy and work, intimately related as they are, use the same unit. Energy comes in a vast array of typ ...
... But what does that mean? Well work is done when something is displaced by a force. If work is done, it takes energy. If you lift a 1 N rock 1 m, you’ve done 1 J of work and expended 1 J of energy. Energy and work, intimately related as they are, use the same unit. Energy comes in a vast array of typ ...
Lecture 9: Solids and Fluids
... has been introduced into the left side (the dashed line is an imaginary barrier). All the molecules move in random direction. Since there are more molecules on the left side, more molecules migrate into the right side than otherwise. Once a concentration equilibrium is reached, there will be no net ...
... has been introduced into the left side (the dashed line is an imaginary barrier). All the molecules move in random direction. Since there are more molecules on the left side, more molecules migrate into the right side than otherwise. Once a concentration equilibrium is reached, there will be no net ...
Levers
... A class 2 lever has the load and the effort on the same side of the fulcrum, with the load nearer the fulcrum. Examples of a class-two lever are a pair of nutcrackers or a wheelbarrow. In the diagram, the wheel or fulcrum on the wheelbarrow is helping to share the weight of the load. This means that ...
... A class 2 lever has the load and the effort on the same side of the fulcrum, with the load nearer the fulcrum. Examples of a class-two lever are a pair of nutcrackers or a wheelbarrow. In the diagram, the wheel or fulcrum on the wheelbarrow is helping to share the weight of the load. This means that ...
05_02
... locus called the moving centrode. Motion of body i may be characterized as pure rolling of the moving centrode on the fixed centrode because body i instantaneously has zero velocity at each location of the ICR. ...
... locus called the moving centrode. Motion of body i may be characterized as pure rolling of the moving centrode on the fixed centrode because body i instantaneously has zero velocity at each location of the ICR. ...
Electromechanical Dynamics, Part 2 - Solution Manual, Woodson Melcher
... the flux density penetrates less and less into the specimen until at high frequencies (- >> 1) the flux density is completely excluded from the conductor. At very low frequencies (d << 1) the flux density penetrates completely and is essentially unaffected by the presence of the conducting material. ...
... the flux density penetrates less and less into the specimen until at high frequencies (- >> 1) the flux density is completely excluded from the conductor. At very low frequencies (d << 1) the flux density penetrates completely and is essentially unaffected by the presence of the conducting material. ...
Dyadic Tensor Notation
... and projection operators. (These are mathematical objects which take the projection or component of a vector along a particular direction.) Section C returns to a physical problem (also about polarization) and leads to a discussion of principal axes, eigenvectors and eigenvalues of tensor quantities ...
... and projection operators. (These are mathematical objects which take the projection or component of a vector along a particular direction.) Section C returns to a physical problem (also about polarization) and leads to a discussion of principal axes, eigenvectors and eigenvalues of tensor quantities ...
practice questions for chapters 12-14
... 4. What is the force F needed to just lift the ball off the floor? A) 0.5 mg B) 1.41 mg C) 1.73 mg D) mg E) None of these is correct. Ans: C 5. What is the magnitude of the force the contact point c exerts on the ball when the applied force F just lifts the ball off the floor? A) mg B) 1.5 mg C) 1.7 ...
... 4. What is the force F needed to just lift the ball off the floor? A) 0.5 mg B) 1.41 mg C) 1.73 mg D) mg E) None of these is correct. Ans: C 5. What is the magnitude of the force the contact point c exerts on the ball when the applied force F just lifts the ball off the floor? A) mg B) 1.5 mg C) 1.7 ...
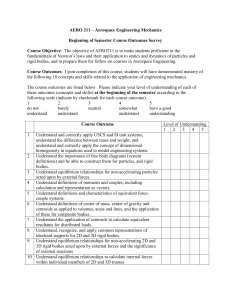
Outcomes Survey Begi.. - Aerospace Engineering Courses page
... Understand and correctly apply USCS and SI unit systems, understand the difference between mass and weight, and understand and correctly apply the concept of dimensional homogeneity in equations used to model engineering systems. 2 Understand the importance of free body diagrams (system definitions) ...
... Understand and correctly apply USCS and SI unit systems, understand the difference between mass and weight, and understand and correctly apply the concept of dimensional homogeneity in equations used to model engineering systems. 2 Understand the importance of free body diagrams (system definitions) ...
Newton`s third law
... Pulleys: The velocity of the masses is equal to the radius times the angular velocity of the pulley (as are the linear and angular accelerations Rigid body: All points at a given distance from the pulley center have the same acceleration. ...
... Pulleys: The velocity of the masses is equal to the radius times the angular velocity of the pulley (as are the linear and angular accelerations Rigid body: All points at a given distance from the pulley center have the same acceleration. ...
Circular Motion and Gravitation Newton*s Law of Gravitation
... the sun, have many layers – kind of like an onion: In other words, NONE of the celestial bodies we observe are point masses. Given that the law is called the universal law of gravitation, how do we use it for planets and such? ...
... the sun, have many layers – kind of like an onion: In other words, NONE of the celestial bodies we observe are point masses. Given that the law is called the universal law of gravitation, how do we use it for planets and such? ...
Classical central-force problem
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System.