Ch6. Work Done by a Constant Force
... 125 N). That opposes her motion, and a normal force FN (magnitude =612 N). Determine the net work done by the three forces when she coasts for a distance of ...
... 125 N). That opposes her motion, and a normal force FN (magnitude =612 N). Determine the net work done by the three forces when she coasts for a distance of ...
Newton`s Laws of Motion
... universe can be explained by the same few rules. His mathematical analysis of gravitational force and motion showed that planetary orbits had to be the very ellipses that Kepler had proposed two generations earlier. ● Understand that Newton’s system was based on the concepts of mass, force, and acce ...
... universe can be explained by the same few rules. His mathematical analysis of gravitational force and motion showed that planetary orbits had to be the very ellipses that Kepler had proposed two generations earlier. ● Understand that Newton’s system was based on the concepts of mass, force, and acce ...
Physics Notes Class 11 CHAPTER 8 GRAVITATION
... (i) Unlike the electrostatic force, it is independent of the medium between the particles. (ii) It is conservative in nature. (iii) It expresses the force between two point masses (of negligible volume). However, for external points of spherical bodies the whole mass can be assumed to be concentrate ...
... (i) Unlike the electrostatic force, it is independent of the medium between the particles. (ii) It is conservative in nature. (iii) It expresses the force between two point masses (of negligible volume). However, for external points of spherical bodies the whole mass can be assumed to be concentrate ...
Newton`s 2d Law of Motion
... gravitational field strength and is expressed as 9.8 N/kg (for a location upon Earth's surface). • Because the 9.8 N/kg gravitational field at Earth's surface causes a 9.8 m/s/s acceleration of any object placed there, we often call this ratio the acceleration of gravity. ...
... gravitational field strength and is expressed as 9.8 N/kg (for a location upon Earth's surface). • Because the 9.8 N/kg gravitational field at Earth's surface causes a 9.8 m/s/s acceleration of any object placed there, we often call this ratio the acceleration of gravity. ...
Physics
... rotating force Fr b. when r is not perpendicular to Fr, then = rFrsin c. torque units are m•N (not N•m—work) First Law: Object remains at rest or uniform rotation as long as no net torque (net) acts on it a. measured as the moment of inertia, I = mr2 b. corrects for mass distribution ( = 1 f ...
... rotating force Fr b. when r is not perpendicular to Fr, then = rFrsin c. torque units are m•N (not N•m—work) First Law: Object remains at rest or uniform rotation as long as no net torque (net) acts on it a. measured as the moment of inertia, I = mr2 b. corrects for mass distribution ( = 1 f ...
1-17 The Universal Law of Gravitation
... 17 The Universal Law of Gravitation Consider an object released from rest an entire moon’s diameter above the surface of the moon. Suppose you are asked to calculate the speed with which the object hits the moon. This problem typifies the kind of problem in which students use the universal law of gr ...
... 17 The Universal Law of Gravitation Consider an object released from rest an entire moon’s diameter above the surface of the moon. Suppose you are asked to calculate the speed with which the object hits the moon. This problem typifies the kind of problem in which students use the universal law of gr ...
Question 5 - Dominican
... between two bodies, A and B, the following was recorded. Mass of A is o.2 Kg Mass of B is 0.4 Kg Before the collision, body A moves 0.45 m in 0.3 s. Before the collision, body B is at rest. After the collision, bodies A and B move 0.45 m in 0.9 s. Using the data, verify the principle of conservation ...
... between two bodies, A and B, the following was recorded. Mass of A is o.2 Kg Mass of B is 0.4 Kg Before the collision, body A moves 0.45 m in 0.3 s. Before the collision, body B is at rest. After the collision, bodies A and B move 0.45 m in 0.9 s. Using the data, verify the principle of conservation ...
Enhancement mechanisms for optical forces in integrated optics
... with y-odd vector symmetry (electric field primarily in the y-direction for large separations). Frequency is plotted in dimensionless units νa/c, where ν = ω/(2π). k is the magnitude of the wave vector, which is parallel to the waveguide axes. Note that νa/c = a/λ, where λ is the free-space wavelengt ...
... with y-odd vector symmetry (electric field primarily in the y-direction for large separations). Frequency is plotted in dimensionless units νa/c, where ν = ω/(2π). k is the magnitude of the wave vector, which is parallel to the waveguide axes. Note that νa/c = a/λ, where λ is the free-space wavelengt ...
1 Review Part 1 units n
... energy KE = 1/2 mass.V2 at the lowest point h = 0, and no potential energy. • The two energy extremes are equal Stops v=0 at high point, fastest but h = 0 at low point. Without friction, the kinetic energy at the lowest spot (1) equals the potential energy at the highest spot, and the pendulum will ...
... energy KE = 1/2 mass.V2 at the lowest point h = 0, and no potential energy. • The two energy extremes are equal Stops v=0 at high point, fastest but h = 0 at low point. Without friction, the kinetic energy at the lowest spot (1) equals the potential energy at the highest spot, and the pendulum will ...
phys1441-spring09
... the point that is displaced 57m downhill. What are the forces in this motion? Gravitational force: Fg Normal force: FN ...
... the point that is displaced 57m downhill. What are the forces in this motion? Gravitational force: Fg Normal force: FN ...
Higher Physics – Unit 2
... large body, the mass must be given enough kinetic energy so that when it reaches “infinity” its kinetic energy is 0. ...
... large body, the mass must be given enough kinetic energy so that when it reaches “infinity” its kinetic energy is 0. ...
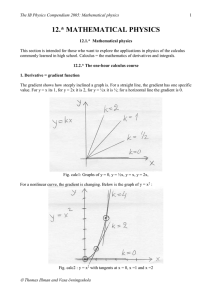
12. MATHEMATICAL PHYSICS
... Example 1: Simple derivative Since v = ds/dt and s = vdt we can for a constant acceleration take v = u +at and get s = (u+at)dt which with conventional integrating rules gives the familiar s = ut + ½at2. Example 2: Inner derivative We have seen the formula P = Fv and used it for situations of con ...
... Example 1: Simple derivative Since v = ds/dt and s = vdt we can for a constant acceleration take v = u +at and get s = (u+at)dt which with conventional integrating rules gives the familiar s = ut + ½at2. Example 2: Inner derivative We have seen the formula P = Fv and used it for situations of con ...
Classical central-force problem
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System.