Help Section - AdvancedPlacementPhysicsC
... the statics of rigid bodies. The situation described on the first slide is static as long as the man is not more than one-third of the way up the ladder, because there is no motion. Therefore, the conditions for static equilibrium apply to the situation. What are the static equilibrium conditions? ...
... the statics of rigid bodies. The situation described on the first slide is static as long as the man is not more than one-third of the way up the ladder, because there is no motion. Therefore, the conditions for static equilibrium apply to the situation. What are the static equilibrium conditions? ...
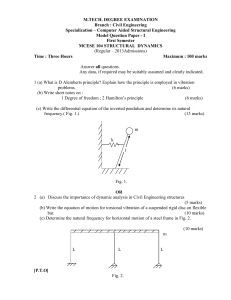
mcese 104 structural dynamics
... centre. The rotor in the machine generates a harmonic force of 3,000 kg. at a frequency 60 rad/sec. Assume 10% damping, calculate amplitude of motion of machine, force transmitted to supports and phase angle. Span of beam 3m ,E – 2 x 105 Mpa and I of beam 5000 cm4. (12 marks) ...
... centre. The rotor in the machine generates a harmonic force of 3,000 kg. at a frequency 60 rad/sec. Assume 10% damping, calculate amplitude of motion of machine, force transmitted to supports and phase angle. Span of beam 3m ,E – 2 x 105 Mpa and I of beam 5000 cm4. (12 marks) ...
rotational inertia - Cardinal Newman High School
... – This is analogous to “inertia of motion”, which was momentum. • Angular momentum rotational inertia angular velocity – This is analogous to Linear momentum mass velocity ...
... – This is analogous to “inertia of motion”, which was momentum. • Angular momentum rotational inertia angular velocity – This is analogous to Linear momentum mass velocity ...
10-12 Circular Rotational Motion
... – This is analogous to “inertia of motion”, which was momentum. • Angular momentum rotational inertia angular velocity – This is analogous to Linear momentum mass velocity ...
... – This is analogous to “inertia of motion”, which was momentum. • Angular momentum rotational inertia angular velocity – This is analogous to Linear momentum mass velocity ...
Momentum - WebPhysics
... • You have probably used the word momentum tossed out in everyday life – but not necessarily 100% correctly. • With a neighbor discuss where you have heard momentum talked about, and try to figure out from that what the average person probably thinks momentum means. ...
... • You have probably used the word momentum tossed out in everyday life – but not necessarily 100% correctly. • With a neighbor discuss where you have heard momentum talked about, and try to figure out from that what the average person probably thinks momentum means. ...
Problem 1 - Department of Physics and Astronomy : University of
... My friend Zodork comes from another planet. In fact, his home planet has two suns. In other words, Zodork's world is situated in a binary star system. Each of the two stars in this system has a mass M. Each star moves in a circle of radius R in such a fashion that the other star is always situated e ...
... My friend Zodork comes from another planet. In fact, his home planet has two suns. In other words, Zodork's world is situated in a binary star system. Each of the two stars in this system has a mass M. Each star moves in a circle of radius R in such a fashion that the other star is always situated e ...
Chapter 7 - Circular Motion
... Angular Displacement (θ) - the angle through which a point is rotated Angular Speed (ω) – the rate at which a body rotates around an axis (rotations per minute = rpm) Radial Distance (r) (radius) - distance from the central axis (center) ...
... Angular Displacement (θ) - the angle through which a point is rotated Angular Speed (ω) – the rate at which a body rotates around an axis (rotations per minute = rpm) Radial Distance (r) (radius) - distance from the central axis (center) ...
Normal, Tension, and Other Examples of Forces
... tension) and TR (right tension), as illustrated. It is reasonable to neglect the weight of ...
... tension) and TR (right tension), as illustrated. It is reasonable to neglect the weight of ...
one-body diagrams and contact forces
... Rule 3: Include only forces exerted on the object. Omit forces exerted by it on other objects. Example: A block is suspended by a rope from the ceiling of an elevator that is accelerating vertically upward (Fig. 4). How many forces act on the block? Two: the non-contact gravitational force of the ea ...
... Rule 3: Include only forces exerted on the object. Omit forces exerted by it on other objects. Example: A block is suspended by a rope from the ceiling of an elevator that is accelerating vertically upward (Fig. 4). How many forces act on the block? Two: the non-contact gravitational force of the ea ...
Ch 8 – Oscillation
... from its equilibrium position. It moves as far on one side as it does on the other. • The time that it takes to make one complete repetition or cycle is called the period of the motion. We will usually measure the period in seconds. • Frequency is the number of cycles per second that an oscillator g ...
... from its equilibrium position. It moves as far on one side as it does on the other. • The time that it takes to make one complete repetition or cycle is called the period of the motion. We will usually measure the period in seconds. • Frequency is the number of cycles per second that an oscillator g ...
Prep 1 - Physics | Oregon State University
... Both P and Q are positive charges; their field lines radiate outward. And Q > P ; Q creates more field lines at any given radial distance from it (this is used to represent a stronger field). (ii) Where in the diagram is the electric field magnitude strongest —and w ...
... Both P and Q are positive charges; their field lines radiate outward. And Q > P ; Q creates more field lines at any given radial distance from it (this is used to represent a stronger field). (ii) Where in the diagram is the electric field magnitude strongest —and w ...
Chap04-2014
... ideal case of zero resistance, horizontal motion would never stop. Galileo was the first to recognize that the general principles of motion could be found by extrapolating experimental results to the ideal case, in which there is no resistance to slow down an object’s motion. ...
... ideal case of zero resistance, horizontal motion would never stop. Galileo was the first to recognize that the general principles of motion could be found by extrapolating experimental results to the ideal case, in which there is no resistance to slow down an object’s motion. ...
Lec12
... the flow of air through a jet engine. The principle of impulse and momentum is applied to a system S of particles during a time interval Dt, including particles which enter the system at A during that time interval and those (of the same mass Dm) which leave the system at B. The system formed by the ...
... the flow of air through a jet engine. The principle of impulse and momentum is applied to a system S of particles during a time interval Dt, including particles which enter the system at A during that time interval and those (of the same mass Dm) which leave the system at B. The system formed by the ...
Classical central-force problem
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System.