1 Simple harmonic motion related to circular motion
... We know that the potential energy function for a spring is (1/2)kx2 , which we found by taking the area under the curve of the force function F = kx (recall, this is force on the spring, so there is no negative sign.) Another way to describe conditions for SHO is that the potential energy function i ...
... We know that the potential energy function for a spring is (1/2)kx2 , which we found by taking the area under the curve of the force function F = kx (recall, this is force on the spring, so there is no negative sign.) Another way to describe conditions for SHO is that the potential energy function i ...
Λ - Piazza
... • Ordinary differential equations: a relation that contains functions of only one independent variable, and one or more of its derivatives with respect to that variable. (e.g. Newton’s second law) • Euler integration: a first-order numerical procedure for solving ordinary differential equations (ODE ...
... • Ordinary differential equations: a relation that contains functions of only one independent variable, and one or more of its derivatives with respect to that variable. (e.g. Newton’s second law) • Euler integration: a first-order numerical procedure for solving ordinary differential equations (ODE ...
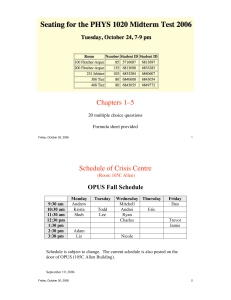
Chapters 1–5 Schedule of Crisis Centre
... • Elastic collision: the total kinetic energy after collision is equal ! to the total before collision. • Inelastic collision: the total kinetic energy is not conserved. If ! objects stick together after collision, the collision is “perfectly ! inelastic” – no bounce of one object from the other. Ex ...
... • Elastic collision: the total kinetic energy after collision is equal ! to the total before collision. • Inelastic collision: the total kinetic energy is not conserved. If ! objects stick together after collision, the collision is “perfectly ! inelastic” – no bounce of one object from the other. Ex ...
Lecture 18
... • In this chapter (10) we are going to look at rotational motion. • First, we need to go back and review the nomenclature we use to describe rotational motion. • Motion of an object can be described by translational motion of the CM + rotation of the object around its CM! 95.141, F2010, Lecture 18 ...
... • In this chapter (10) we are going to look at rotational motion. • First, we need to go back and review the nomenclature we use to describe rotational motion. • Motion of an object can be described by translational motion of the CM + rotation of the object around its CM! 95.141, F2010, Lecture 18 ...
fan cart physics
... below. 1. Look at the blue lines coming from the fan. In which direction is the air pushed? ____________________ 2. Press Play ( ) and observe the cart. In which direction does the cart move? __________________ By blowing to the left, the fans exert a force on the cart that pushes it to the right. T ...
... below. 1. Look at the blue lines coming from the fan. In which direction is the air pushed? ____________________ 2. Press Play ( ) and observe the cart. In which direction does the cart move? __________________ By blowing to the left, the fans exert a force on the cart that pushes it to the right. T ...
Forces - Cloudfront.net
... (small black projectile) is hit, the puck travels at nearly the same speed and in a straight line across the ice. All real objects are subject to friction for anything sliding on a surface, and an icy surface is as close to frictionless as we can get. ...
... (small black projectile) is hit, the puck travels at nearly the same speed and in a straight line across the ice. All real objects are subject to friction for anything sliding on a surface, and an icy surface is as close to frictionless as we can get. ...
Slide 1
... Newton’s second law states that if no net force is exerted on a system, no acceleration occurs. Does it follow that no change in momentum occurs? Answer: Yes, because no acceleration means that no change occurs in velocity or in momentum (mass × velocity). Another line of reasoning is simply that no ...
... Newton’s second law states that if no net force is exerted on a system, no acceleration occurs. Does it follow that no change in momentum occurs? Answer: Yes, because no acceleration means that no change occurs in velocity or in momentum (mass × velocity). Another line of reasoning is simply that no ...
SEC - Warrenphysics
... (Hint: What are the speeds at those times?) 11. Figure 7-26 shows three forces applied to a trunk that moves leftward by 3.00 m over a frictionless floor. The force magnitudes are F1 = 5.00 N, F2 = 9.00 N, and F3 = 3.00 N. During the displacement, a. what is the net work done on the trunk by the thr ...
... (Hint: What are the speeds at those times?) 11. Figure 7-26 shows three forces applied to a trunk that moves leftward by 3.00 m over a frictionless floor. The force magnitudes are F1 = 5.00 N, F2 = 9.00 N, and F3 = 3.00 N. During the displacement, a. what is the net work done on the trunk by the thr ...
Wells Problem Workbook Pack
... from start to the point in question and add the absolute values of the areas (ignore negatives). - AVERAGE velocity or speed over 1 individual segment only use v(bar) = (Vi + Vf) / 2 (velocity would have a direction, speed would not) or v(bar) = d / t (d = displacement for velocity, d = distance for ...
... from start to the point in question and add the absolute values of the areas (ignore negatives). - AVERAGE velocity or speed over 1 individual segment only use v(bar) = (Vi + Vf) / 2 (velocity would have a direction, speed would not) or v(bar) = d / t (d = displacement for velocity, d = distance for ...
Grade 5 - Detroit Public Schools
... - Forces acting on an object in opposing directions of unequal strength are unbalanced (non-zero net force). - An object at rest will begin to move if a non-zero net force is applied to it. It will move in the direction of the non-zero net force. - An object that is in motion will speed up, slow dow ...
... - Forces acting on an object in opposing directions of unequal strength are unbalanced (non-zero net force). - An object at rest will begin to move if a non-zero net force is applied to it. It will move in the direction of the non-zero net force. - An object that is in motion will speed up, slow dow ...
6 ppt Momentum and Collisions
... After they collide there velocities become v1f and v2f. The impulse-momentum theorem FΔt = Δp describes their change in momentum. Newton’s third law tells us the force acting on these cars is equal and opposite. ...
... After they collide there velocities become v1f and v2f. The impulse-momentum theorem FΔt = Δp describes their change in momentum. Newton’s third law tells us the force acting on these cars is equal and opposite. ...
Collisions and rotational kinematics
... rotating object, we need r and either θ or ω. What is the speed of the tire rim if the radius r s is 0.35 m and the tire rotates at 20 rad/s? θ Radians measure distance around a unit circle Therefore s = rθ (only for θ in radians!) ds dθ =r Time derivative of both sides (r is constant): dt dt v = rω ...
... rotating object, we need r and either θ or ω. What is the speed of the tire rim if the radius r s is 0.35 m and the tire rotates at 20 rad/s? θ Radians measure distance around a unit circle Therefore s = rθ (only for θ in radians!) ds dθ =r Time derivative of both sides (r is constant): dt dt v = rω ...
Bumper Cars Observations about Bumper Cars
... Moving cars tend to stay moving Changing a car’s motion takes time Impacts alter velocities and angular velocities Cars often appear to exchange their motions The fullest cars are the hardest to redirect The least-full cars get slammed during collisions ...
... Moving cars tend to stay moving Changing a car’s motion takes time Impacts alter velocities and angular velocities Cars often appear to exchange their motions The fullest cars are the hardest to redirect The least-full cars get slammed during collisions ...
Rotational Inertia Demonstrator
... dimensions of the various parts of the system. Since all the thin rods and moveable masses are the same you only need to measure one of each. The moveable masses on the rods are treated as point-masses and have the same formula for moment of inertia as a hoop. Unscrew one of the thin rods and find a ...
... dimensions of the various parts of the system. Since all the thin rods and moveable masses are the same you only need to measure one of each. The moveable masses on the rods are treated as point-masses and have the same formula for moment of inertia as a hoop. Unscrew one of the thin rods and find a ...
Final Momentum NRG Review
... EXAMPLE: How much work is done by a girl in taking a 7.5 kg bowling ball from a shelf and lowering it 2.0 meters to the floor? Note, that gravity is pulling the bowling ball downwards and it’s the force exerted against this gravitational force that allows the ball to be lowered rather than accelerat ...
... EXAMPLE: How much work is done by a girl in taking a 7.5 kg bowling ball from a shelf and lowering it 2.0 meters to the floor? Note, that gravity is pulling the bowling ball downwards and it’s the force exerted against this gravitational force that allows the ball to be lowered rather than accelerat ...
Classical central-force problem
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System.