Particle acceleration by electric field in an 3D RCS
... Particle acceleration by electric field in an 3D RCS Valentina Zharkova and Mykola Gordovskyy ...
... Particle acceleration by electric field in an 3D RCS Valentina Zharkova and Mykola Gordovskyy ...
Quantum Mathematics
... instead seek a field theoretic foundation for mathematics. • A Feynman diagram (let’s take cubic interactions) has the same structure as a proof in a formal system X: two things come together and a third thing gets “spit out.” A⇒ B ...
... instead seek a field theoretic foundation for mathematics. • A Feynman diagram (let’s take cubic interactions) has the same structure as a proof in a formal system X: two things come together and a third thing gets “spit out.” A⇒ B ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 17. (i)Explain the principle and working of electron microscope. (ii) Outline an idealised experiment to bring out the significance of Heisenberg’s uncertainty principle. 18.State and prove Ehernfest’s theorem. 19.Deduce expressions for the Eigen values of the square of the total angular momentum an ...
... 17. (i)Explain the principle and working of electron microscope. (ii) Outline an idealised experiment to bring out the significance of Heisenberg’s uncertainty principle. 18.State and prove Ehernfest’s theorem. 19.Deduce expressions for the Eigen values of the square of the total angular momentum an ...
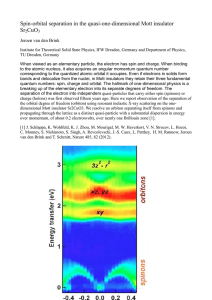
Spin-orbital separation in the quasi-one
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
α | Q | β 〉= Q (t) . 〈 Review
... interactions, possibly having small effects. {Usually H0 is a single particle operator; and H1 is a two-particle operator describing the interactions between particles.} ...
... interactions, possibly having small effects. {Usually H0 is a single particle operator; and H1 is a two-particle operator describing the interactions between particles.} ...
Phys202_Exam3_2006.doc
... 18. There are how many different states of polarization for an e-m wave? a. 1 b. ~ 2 c. 3 d. 4 ...
... 18. There are how many different states of polarization for an e-m wave? a. 1 b. ~ 2 c. 3 d. 4 ...
Quantum Mechanics I. Introduction Just before 1900, the classical
... Just before 1900, the classical physics of Newton and Maxwell was unable to explain certain phenomena. The result was a major revolution in physics, the development of quantum mechanics. We no longer see the world as precisely definable, but there is an inherent uncertainty and fuzziness to nature. ...
... Just before 1900, the classical physics of Newton and Maxwell was unable to explain certain phenomena. The result was a major revolution in physics, the development of quantum mechanics. We no longer see the world as precisely definable, but there is an inherent uncertainty and fuzziness to nature. ...
Lesson 1 - Tarleton State University
... wave but interacts as a particle as claimed by Einstein then particles must also have wave properties! Furthermore, the basic equations must be analogous since all particles are waves and vice-versa. ...
... wave but interacts as a particle as claimed by Einstein then particles must also have wave properties! Furthermore, the basic equations must be analogous since all particles are waves and vice-versa. ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI M.Sc. THIRD
... 19. Set up the Schrodinger wave equation for a linear harmonic harmonic oscillator and obtain the energy eigenfunctions. Plot the eigenfunctions and probability density distribution as a function of ‘x’ for the lowest two energy ...
... 19. Set up the Schrodinger wave equation for a linear harmonic harmonic oscillator and obtain the energy eigenfunctions. Plot the eigenfunctions and probability density distribution as a function of ‘x’ for the lowest two energy ...
Foundations of Classical and Quantum Electrodynamics Brochure
... 1 The Mathematical Methods of Electrodynamics 1 1.1 Vector and Tensor Algebra 1 1.1.1 The Definition of a Tensor and Tensor Operations 1 1.1.2 The Principal Values and Invariants of a Symmetric Tensor of Rank 2 8 1.1.3 Covariant and Contravariant Components 11 1.1.4 Tensors in Curvilinear and Nonort ...
... 1 The Mathematical Methods of Electrodynamics 1 1.1 Vector and Tensor Algebra 1 1.1.1 The Definition of a Tensor and Tensor Operations 1 1.1.2 The Principal Values and Invariants of a Symmetric Tensor of Rank 2 8 1.1.3 Covariant and Contravariant Components 11 1.1.4 Tensors in Curvilinear and Nonort ...
String Theory
... would happen if you performed certain experiments. Theorists are usually exploring areas that are so advanced that modern technology would not allow you to conduct an experiment on the theoretical topic. ...
... would happen if you performed certain experiments. Theorists are usually exploring areas that are so advanced that modern technology would not allow you to conduct an experiment on the theoretical topic. ...
Renormalization

In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities.Renormalization specifies relationships between parameters in the theory when the parameters describing large distance scales differ from the parameters describing small distances. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in infinities. When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, this continuum limit, the removal of the ""construction scaffolding"" of lattices at various scales, has to be taken carefully, as detailed below.Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through ""effective"" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each.