Lagrangians
... which is what we might have expected from the non-relativistic results. Why the minus sign? Well, it has to do with the metric. The upper index contravariant momentum has to be the derivative with respect to the lower index, covariant velocity and vice versa. The space part changes sign und ...
... which is what we might have expected from the non-relativistic results. Why the minus sign? Well, it has to do with the metric. The upper index contravariant momentum has to be the derivative with respect to the lower index, covariant velocity and vice versa. The space part changes sign und ...
Lecture 7: Why is Quantum Gravity so Hard?
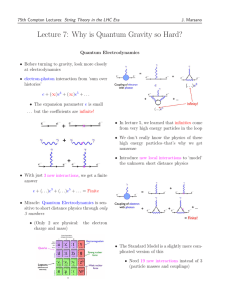
... • Before turning to gravity, look more closely at electrodynamics • electron-photon interaction from ’sum over histories’ e + (∞)e3 + (∞)e5 + . . . • The expansion parameter e is small . . . but the coefficients are infinite! • In lecture 5, we learned that infinities come from very high energy part ...
... • Before turning to gravity, look more closely at electrodynamics • electron-photon interaction from ’sum over histories’ e + (∞)e3 + (∞)e5 + . . . • The expansion parameter e is small . . . but the coefficients are infinite! • In lecture 5, we learned that infinities come from very high energy part ...
Historic Development by Mihai
... threshold wavelength which is specific to the material. Especially the fact that light of large wavelengths has no effect at all even if it is extremely intensive, appeared mysterious for the scientists. Albert Einstein finally gave the explanation in 1905: Light consists of particles (photons), and ...
... threshold wavelength which is specific to the material. Especially the fact that light of large wavelengths has no effect at all even if it is extremely intensive, appeared mysterious for the scientists. Albert Einstein finally gave the explanation in 1905: Light consists of particles (photons), and ...
Worksheet - 1 - International Indian School, Riyadh
... 7. How many unpaired electrons are present in N? Name the principle which explains the presence of these unpaired electrons. 2 or more marks Question: 8. Write a short note on Plank’s Quantum theory. 9. Calculate the wavelength of an electron that has been accelerated in a particle accelerator throu ...
... 7. How many unpaired electrons are present in N? Name the principle which explains the presence of these unpaired electrons. 2 or more marks Question: 8. Write a short note on Plank’s Quantum theory. 9. Calculate the wavelength of an electron that has been accelerated in a particle accelerator throu ...
By convention magnetic momentum of a current loop is calculated by
... The particles radius in the electric field spin direction may be calculated by: ...
... The particles radius in the electric field spin direction may be calculated by: ...
Ideas of Modern Physics
... 16. A pure semiconductor is an insulator, but becomes useful electrically when a. it is cooled to low temperature b. not too large a magnetic field is applied c. some of its atoms are replaced with different atoms d. quantum states are created in it e. it is patterned to very small (nanometer) sizes ...
... 16. A pure semiconductor is an insulator, but becomes useful electrically when a. it is cooled to low temperature b. not too large a magnetic field is applied c. some of its atoms are replaced with different atoms d. quantum states are created in it e. it is patterned to very small (nanometer) sizes ...
Abstract
... mentioned above acquire a physical interpretation. Moreover, the predictive success of quantum mechanics is explained, but in some cases (in particular, if proper mixtures are considered) the predictions of the two theories are substantially different, which suggests new possible experiments to chec ...
... mentioned above acquire a physical interpretation. Moreover, the predictive success of quantum mechanics is explained, but in some cases (in particular, if proper mixtures are considered) the predictions of the two theories are substantially different, which suggests new possible experiments to chec ...
Renormalization

In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities.Renormalization specifies relationships between parameters in the theory when the parameters describing large distance scales differ from the parameters describing small distances. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in infinities. When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, this continuum limit, the removal of the ""construction scaffolding"" of lattices at various scales, has to be taken carefully, as detailed below.Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through ""effective"" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each.