The Differential Geometry and Physical Basis for the Application of
... turned from trying to unify electromagnetism and gravity to introducing as a phase factor an exponential in which the phase α is preceded by the imaginary unit i, e.g., e+iqα(x), in the wave function for the wave equations (for instance, the Dirac equation is (iγμ∂μ −m)ψ = 0). It is here that Weyl c ...
... turned from trying to unify electromagnetism and gravity to introducing as a phase factor an exponential in which the phase α is preceded by the imaginary unit i, e.g., e+iqα(x), in the wave function for the wave equations (for instance, the Dirac equation is (iγμ∂μ −m)ψ = 0). It is here that Weyl c ...
Generalized Momentum Operators
... If the particle is constrained to move on a ring they we expect ψ(x) ∈ H and all of its derivatives to be periodic—a condition that serves even less problematically to kill all all boundary terms. Problems arise, however, if the particle is constrained to move on a finite interval (confined to the i ...
... If the particle is constrained to move on a ring they we expect ψ(x) ∈ H and all of its derivatives to be periodic—a condition that serves even less problematically to kill all all boundary terms. Problems arise, however, if the particle is constrained to move on a finite interval (confined to the i ...
Basics of Lattice Quantum Field Theory∗
... Discuss how, if U ∈ SU(3), your proposal can be embedded in SU(3) via two or more SU(2) subgroups, such that all SU(3) elements can be reached under multiple moves. This is how many updates in quenched QCD work in principle. ...
... Discuss how, if U ∈ SU(3), your proposal can be embedded in SU(3) via two or more SU(2) subgroups, such that all SU(3) elements can be reached under multiple moves. This is how many updates in quenched QCD work in principle. ...
Neitzke: What is a BPS state?
... The quantum theories we want to understand are describing phenomena which take place in Minkowski space E3,1 . Among other things, such a theory is supposed to have an associated Hilbert space H, whose vectors represent the possible “states” of the system. One simple example of a quantum theory whic ...
... The quantum theories we want to understand are describing phenomena which take place in Minkowski space E3,1 . Among other things, such a theory is supposed to have an associated Hilbert space H, whose vectors represent the possible “states” of the system. One simple example of a quantum theory whic ...
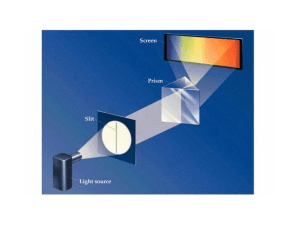
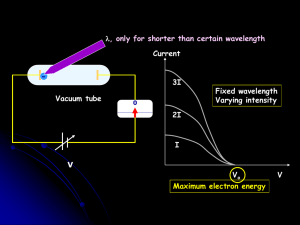
Unified Field Theory
... matter, in all of its variety of forms, can be explained in terms of atoms and the electromagnetic forces between them, realizing Democritus's vision. Quantum mechanics also provides for a theory of the structure of atoms in terms of the electromagnetic forces between the atomic nucleus and the elec ...
... matter, in all of its variety of forms, can be explained in terms of atoms and the electromagnetic forces between them, realizing Democritus's vision. Quantum mechanics also provides for a theory of the structure of atoms in terms of the electromagnetic forces between the atomic nucleus and the elec ...
GAMOW VECTORS IN THE BAKAMJIAN-THOMAS CONSTRUCTION SUJEEV WICKRAMASEKARA
... Unitary representations of the Poincaré group P underlie all physical theories that obey the principles of special relativity and quantum mechanics. The Poincaré group is also fundamental to classical relativistic physics. In this context, Dirac considered the problem of describing interactions betw ...
... Unitary representations of the Poincaré group P underlie all physical theories that obey the principles of special relativity and quantum mechanics. The Poincaré group is also fundamental to classical relativistic physics. In this context, Dirac considered the problem of describing interactions betw ...
Quantum Mechanics: PHL555 Tutorial 2
... part of the Hamiltonian represents the interaction with the magnetic field. We have neglected the effects due to spin angular momentum of the electron . Treat H 1 as a perturbation and show s(l 0) states are not split , where as p(l 1) states are split into three states separated by the energy i ...
... part of the Hamiltonian represents the interaction with the magnetic field. We have neglected the effects due to spin angular momentum of the electron . Treat H 1 as a perturbation and show s(l 0) states are not split , where as p(l 1) states are split into three states separated by the energy i ...
Renormalization

In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities.Renormalization specifies relationships between parameters in the theory when the parameters describing large distance scales differ from the parameters describing small distances. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in infinities. When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, this continuum limit, the removal of the ""construction scaffolding"" of lattices at various scales, has to be taken carefully, as detailed below.Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through ""effective"" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each.