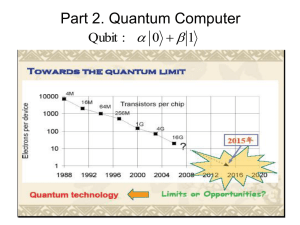
Exam questions - Grand Valley State University
... D. Part of the above diagram is reproduced at right. Three vectors originating from point Y are also shown. The middle vector points directly from point Y to point Z. In order for the particle to be launched from Y and reach Z, which vector best represents the initial velocity of the particle? Clear ...
... D. Part of the above diagram is reproduced at right. Three vectors originating from point Y are also shown. The middle vector points directly from point Y to point Z. In order for the particle to be launched from Y and reach Z, which vector best represents the initial velocity of the particle? Clear ...
Chapter 6 and 7 Reading Guide Electronic Structure of Atoms and
... What is the shape of an s orbital? What is the difference between a 1s, 2s or 3s orbital? ...
... What is the shape of an s orbital? What is the difference between a 1s, 2s or 3s orbital? ...
Coupling Charged Particles to the Electromagnetic Field
... tells us that the amplitude to go from a point A to a point B along a particular classical path is eiS(A,B)/~ . We have seen ~ field. So if we how the action is modified in the presence of a A turn on the solenoid, we the amplitude changes to ...
... tells us that the amplitude to go from a point A to a point B along a particular classical path is eiS(A,B)/~ . We have seen ~ field. So if we how the action is modified in the presence of a A turn on the solenoid, we the amplitude changes to ...
Part VI - TTU Physics
... • For many cases, instead of a an average scattering time t, it’s often necessary to formulate a theory of conductivity in terms of ...
... • For many cases, instead of a an average scattering time t, it’s often necessary to formulate a theory of conductivity in terms of ...
Renormalization

In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities.Renormalization specifies relationships between parameters in the theory when the parameters describing large distance scales differ from the parameters describing small distances. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in infinities. When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, this continuum limit, the removal of the ""construction scaffolding"" of lattices at various scales, has to be taken carefully, as detailed below.Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through ""effective"" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each.