Download Worksheet 38 (7

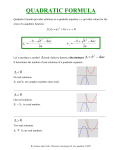
Worksheet 38 (7.1)
Chapter 7 Quadratic Equations and Inequalities
7.1 Complex Numbers
A complex number is any number that can be expressed in the form
a + bi, where a and b are real numbers.
The standard form of a complex number is a + bi. The real number a is
called the real part of the complex number and the real number b is
called the imaginary part of the complex number.
Important definitions involving i:
1. i = - 1
2. i2 = - 1
3. - b = i b
Note: The square root of any negative real number must be
rewritten as an imaginary number before doing any computation.
Summary 1:
Warm-up 1. a) Give the real part and imaginary part of -2 + 5i.
a = _____ b = _____
b) Give the standard form of -5i. _______________
c) Rewrite - 49 as an imaginary number.
- 49 = i
=i ( )
= ______
d) Rewrite - 45 as an imaginary number.
- 45 = i
) or 3 i
=i (
Worksheet 38 (7.1)
Problems
151
1. Give the real part and imaginary part of 2 - 5i.
2. Give the standard form of 7.
3. Rewrite - 100 as an imaginary number.
4. Rewrite - 48 as an imaginary number.
Summary 2:
1. Add
the realnumbers:
parts.
Adding
complex
(a + bi) + (c + di) = (a + c) + (b + d)i
2. Add the imaginary parts.
3. Express in standard form.
Subtracting complex numbers: (a + bi) - (c + di) = (a - c) + (b - d)i
1. Subtract the real parts.
2. Subtract the imaginary parts.
3. Express in standard form.
Warm-up 2. Add or subtract as indicated:
a) (4 - 9i) + (-8 + 3i) = (4 + ____) + (-9 + ____)i
= _____ + _____i
or
___________
b) (-2 - i) - (-1 - 4i) = (-2 - ____) + (-1 - ____)i
= _____ + _____i
Problems - Add or subtract as indicated:
5. (3 + 2i) + (-5 + 7i)
6. (3 + i) - (9 + 4i)
Worksheet 38 (7.1)
Summary 3:
Multiplying complex numbers:
152
1. Follow summary 2 in section 3.3 for multiplying two binomials.
Note: A complex number has a binomial form.
2. Replace i2 with -1.
3. Simplify to express the result in standard form.
Warm-up 3. Find the following products:
a) (2 + 5i)(4 + 3i) = 2(
) + 5i(
)
= _____ + 6i + _____ + 15i2
= 8 + 26i - _____
= ___________
b) (3 - 5i)2 = (
= 3(
)(
)
) - 5i(
)
= _____ - 15i - 15i + _____
= 9 - 30i - _____
= ___________
c) (2 - 7i)(2 + 7i) = 2(
) - 7i(
)
= _____ + 14i - _____ - 49i2
= _____ + 0i + _____
= ___________
Problems - Find the following products:
7. (-2 + 6i)(4 - 3i)
8. (4 - 2i)2
Worksheet 38 (7.1)
9. (1 - 3i)(1 + 3i)
153
Two complex numbers a + bi and a - bi are called conjugates of each other.
Note: The product of a complex number and its conjugate is always a real
number - see warm-up 3c and problem 9 in above summary.
Dividing complex numbers:
1. Determine the conjugate of the denominator.
2. Multiply both numerator and denominator by this conjugate to obtain
an equivalent fraction with a real-number denominator.
3. Express the result in standard form when directed to do so.
Summary 4:
Warm-up 4. Find the following quotients:
a)
b)
2i
5 - 4i
4 - 3i
7 - 2i
( 2i )(
)
(5 - 4i)(
)
2i(
) + 2i(
)
=
2
25 - 16 i
( )- 8
=
25 - ( )
- 8 + 10i
=
( )
=
=
(standard form)
(4 - 3i)(
)
(7 - 2i)(
)
28 + ( ) - ( ) - 6 i 2
=
49 - 4 i 2
28 - ( ) + ( )
=
49 + ( )
=
Worksheet 38 (7.1)
=
(
) - 13i
53
=
c)
7 (7)(
=
5i (5i)(
(standard form)
)
)
154
(
)
(
)
- 35i
=
(
)
=
=
Note: In warm-up 4c, the numerator and denominator could have been multiplied by i to produce
the same result.
Problems - Find the following quotients:
10.
5i
- 3 + 2i
11.
3 - 4i
2+i
12.
- 3 + 2i
5i
Worksheet 39 (7.2)
7.2 Quadratic Equations
A quadratic equation is a second-degree equation in one variable that
contains a variable with an exponent of two.
Summary 1:
155
For quadratic equations of the form x2 = a, where x is a variable and a is any
real number, the following square root property holds true:
For any real number a, x2 = a if and only if x = a or x = - a .
Solving quadratic equations of the form x2 = a:
1. If necessary, rewrite the equation in the form x2 = a.
2. Apply the above square root property: x =  a
3. Solve for x.
4. Write an appropriate solution set.
5. Check when directed to do so.
Warm-up 1. Solve each of the following quadratic equations by applying the
square root property:
a) x 2 = - 16
x=
The solution set is __________.
x=
2
b) (n - 1 ) = 36
n - 1= 
n - 1= 
n - 1 =______ or n - 1 =______
n =______ or n =______
The solution set is __________.
Worksheet 39 (7.2)
2
c) (2y - 3 ) = - 45
2y - 3 = 
2y - 3 =  i
2y - 3 =  3 i
3i 5
2y =
y=
The solution set is ___________.
2
2
d) 2(y + 5 ) - 9
= 41
2
2(y + 5 )
=
(y + 5 )2
=
y+5
=
or y + 5 =
y +5=
156
y=
or y =
The solution set is __________.
Problems - Solve each of the following quadratic equations by applying the square
root property:
1. y 2 = - 49
2. (m - 2 )2 = 16
3. (3x - 2 )2 = - 48
Worksheet 39 (7.2)
4. 3(x + 1 )2 - 10 = 65
Summary 2:
Using the Pythagorean Theorem, summary 3 in section 3.7, can also lead to
solving quadratic equations in the form x2 = a.
Warm-up 2. Set up and write an algebraic equation, then solve:
Note: Drawing a figure is helpful in the word problem which follows.
a) A rectangular parking lot is 25 yards wide. Find, to the nearest yard, the length
of the parking lot if the diagonal is 50 yards long.
Let
x = length of rectangular lot
a2 + b2 = c2
( )2 + 252 = 50 2
2
= 2500
x +
2
x =
x =
157
x
The length of the parking lot is _______ yards.
Problem - Set up and write an algebraic equation, then solve:
5. Find, to the nearest tenth, the length of one side of a square with a diagonal that
is 20 meters long.
Worksheet 40 (7.3)
7.3 Completing the Square
Summary 1:
The coefficient
is often referred
to as
the2 leading
TheNote:
standard
form of a aquadratic
equation
is ax
+ bx + ccoefficient.
= 0, where
a, b, and c are real numbers and a0.
A perfect square trinomial results from squaring a binomial:
(x + a)2 = x2 + 2ax + a2
Note: The constant in a perfect square trinomial is equal to the square
one-half of the coefficient of the x-term.
Rewriting a quadratic equation in the form x2 = a:
1. Put the given equation in standard form.
2. If the leading coefficient is not 1, apply the multiplication property of
equality by dividing each term on both sides by the given leading
coefficient.
3. Apply the addition property of equality to move the constant to the
right side of the equation.
4. Examine the remaining terms on the left side to determine what value
must be added to obtain a perfect square trinomial on the left side
of the equation. This is done by finding the square of one-half of
the coefficient of the x-term.
5. Apply the addition property of equality by adding the result from
step 4 to both sides of the equation.
6. Express the perfect square trinomial found in step 5 as the square of a
binomial.
7. The quadratic equation is now in the form x2 = a where x represents a
binomial and a represents a real number.
158
of
Warm-up 1. Rewrite the given equation in the form x2 = a:
2 y 2 + 8y + 10 = 0
a)
0
2 y2
8y
10
=
+
+
( ) ( ) ( ) ( )
2
y +(
=0
)+ 5
2
=(
y + 4y
)
Worksheet 40 (7.3)
To complete the square for y2 + 4y:
a) ½(4) = 2
b) (2)2 = 4
2
y + 4y + (
) = - 5 +(
2
y + 4y + 4
(
b)
2
x -(
)-(
=(
2
159
)
=-1
)
x
)=0
)
2
= 3x + 10
2
x - 3x = (
)
2
To complete the square for x - 3x:
a) ½(-3) = -32
2
b)  -32  = 94
2
x - 3x + ( ) = 10 + ( )
2
= ( 4 ) + 94
x - 3x + 94
(
2
=
)
49
4
Problems - Rewrite the given equation in the form x2 = a:
1. y 2 - 10y + 28 = 0
2. 2 x2 = 5x + 3
Worksheet 40 (7.3)
Completing the square refers to the method used to solve any quadratic
equation by rewriting it first in the form x2 = a.
Solving quadratic equations by completing the square:
1. Rewrite the quadratic equation in the form x2 = a - see summary 1
above.
2. Apply the square root property: x2 = a if and only if x =  a - see
summary 1 in section 6.2.
3. Solve for x.
4. Write an appropriate solution set.
5. Check when directed to do so.
Summary 2:
Warm-up 2.Solve by completing the square:
160
a)
2
y - 10y + 28
2
=0
=(
y - 10y
2
y - 10y + (
)
) = - 28 + (
2
y - 10y + 25
(
)
=(
)
2
) =-3
y -5 =
) -3
y =(
y =5i
The solution set is _____________.
b)
2 x2
2 x2 - ( ) - ( ) = 0
2 x2
5x
3
0
=
( ) ( ) ( ) ( )
= 5x + 3
Worksheet 40 (7.3)
2
x - 52 x - (
2
x - 52 x
) =0
= 32
2
) = 32 + (
x - 52 x + (
2
25
= ( 16
x - 52 x + 16
(
)
)
2
49
) = 16
x - 45 = 
)
x - 45 =  (
5
5
x- 4=
or x - 4 =
or
x=
The solution set is __________.
Problems - Solve by completing the square:
3. 3 x2 = 14x + 5
161
x=
4. y 2 + 8y + 25 = 0
Worksheet 41 (7.4)
7.4 The Quadratic Formula
Summary 1:
The quadratic formula is derived from completing the square to solve
ax2 + bx + c = 0 for x.
The quadratic formula is used to solve any quadratic equation in standard
form.
The Quadratic Formula:
- b  b2 - 4ac
2a
Note: Since the quadratic formula is frequently used in algebra, it is
common to memorize the formula for instant recall.
Given ax2 + bx + c = 0, x =
Using the quadratic formula to solve any quadratic equation:
1. If necessary, rewrite the given equation in standard form:
ax2 + bx + c = 0
2. Identify a, b, and c from the standard form.
- b  b2 - 4ac
2a
4. Substitute a, b, and c in the quadratic formula to evaluate x.
5. Write an appropriate solution set.
6. Check when directed to do so.
3. Recall the quadratic formula: x =
162
Warm-up 1. Solve using the quadratic formula:
2
a)
x + 2x = 2
2
x + 2x - 2 = ( ) ; a = ____, b = ____, c = ____
x=
x=
- b  b2 - 4ac
2a
-(
) (
2
) - 4(
2( )
)(
)
Worksheet 35 (7.4)
)  4 +( )
2
-2
x=
2
-2 2
x=
2
2(
)
x=
2
The solution set is ____________.
x=
x=
(
163
b)
2y(y + 3) = - 17
2
y +
y=
y=
y=
y=
= 0 ; a = ____, b = ____, c = ____
y+
- b  b2 - 4ac
2a
) (
-(
(
2
) - 4(
2( )
) (
)-(
)(
)
)
4
-6 
4
-6 (
y=
4
2(
y=
4
y=
)
)
The solution set is ____________.
Worksheet 41 (7.4)
c)
6 n2 - 5n - 25 = 0 ; a = ____, b = ____, c = ____
n=
n=
n=
-b 
-(
2
b - 4ac
2a
) (
5 (
(
2
) - 4(
2( )
)+(
)
)(
)
)
5
12
5 (
)
n=
12
5 +(
)
5 -(
)
n=
or n =
12
12
or n =
n=
n=
The solution set is __________.
Note: 6n2 - 5n - 25 = 0 can also be solved by factoring 6n2 - 5n - 25. Try it.
164
Problems - Solve using the quadratic formula:
1. x2 + 7 = 3x
2. 2x2 + 5x = 3
3. 4x2 - 20x + 25 = 0
Worksheet 41 (7.4)
The root of an equation is another name for solution.
Summary 2:
165
The discriminant is the number which appears under the radical sign
(radicand) in the quadratic formula: b2 - 4ac.
The discriminant indicates the kind of roots a quadratic equation will have.
It allows for looking ahead to tell the type of solution that can be expected.
Nature of roots for ax2 + bx + c = 0:
1. If b2 - 4ac < 0, then the equation has two nonreal complex solutions.
2. If b2 - 4ac = 0, then the equation has one real solution with
multiplicity of two.
3. If b2 - 4ac > 0, then the equation has two real solutions.
Evaluating the discriminant to determine the nature of the roots for a
quadratic equation:
1. Rewrite equation in standard form: ax2 + bx + c = 0
2. Identify a, b, and c from the standard form.
3. Recall the expression for the discriminant: b2 - 4ac
4. Substitute a, b, and c and evaluate the expression.
5. Use this value to compare to 0, see list above, and determine the type
of solution that will be obtained.
Note: The equation can be solved to verify the conclusions made using
the discriminant.
166
Warm-up 2. Use the discriminant to determine the nature of the roots:
a) x2 + 5x - 24 = 0 ; a = ____, b = ____, c = ____
b2 - 4ac = ( )2 - 4( )(
= 25 + ( )
= _____
)
Circle the true statement:
121 < 0 ; two nonreal complex solutions
121 = 0 ; one real solution with a multiplicity of two
121 > 0 ; two real solutions
Therefore, x2 + 5x - 24 = 0 has _______________ solutions.
Worksheet 41 (7.4)
b)
2y2 + 17 = 6y
____________________ = 0 ; a = ____, b = ____, c = ____
b2 - 4ac = ( )2 - 4( )(
= _____ - 136
= _____
)
Circle the true statement:
-100 < 0 ; two nonreal complex solutions
-100 = 0 ; one real solution with multiplicity of two
-100 > 0 ; two real solutions
Therefore, 2y2 + 17 = 6y has ______________________ solutions.
Problems - Use the discriminant to determine the nature of the roots:
4. 9x2 - 12x = 60
5. x2 + 12x + 36 = 0
167
Summary 3:
All quadratic equations have two roots, x1 and x2.
Note: When b2 - 4ac = 0, there is one real solution with a multiplicity of
two. This means that the two roots are equal.
Given ax2 + bx + c = 0 with roots x1 and x2, the two following relationships
hold true:
b
1. Sum of the Roots: x1 + x2 = a
c
2. Product of the Roots: (x1)(x2) =
a
Both of these relationships can be tested. If both test true, then the values
are in the solution set. The sum and product of the roots can be
used to replace traditional checking which may be cumbersome
with irrational or complex roots.
Worksheet 41 (7.4)
Warm-up 3. Use the sum and product of the roots to check the previously solved
equations:
a) y2 - 10y + 28 = 0 (See warm-up 2(a) in section 6.3.)
Solution Set = 5 + i 3 , 5 - i 3


x1 + x2 = -
Sum of the Roots:
(
168
)+(
)=
-(
(
b
a
)
)
10 = 10
Product of the Roots:
( x1 )( x 2 ) =
(
( )
( )
) = 28
28 = 28
)=
)(
(
c
a
)+(
Problems - Use the sum and product of the roots to check the previously solved
equations:
6. 6n2 - 5n - 25 = 0 (See warm-up 1(c) in this section.)
Solution Set =  156 , - 53 
7. x2 + 2x = 2 (See warm-up 1(a) in this section.)
Solution Set = - 1 + 3 , - 1 - 3


Worksheet 42 (7.5)
7.5 More Quadratic Equations and Applications
Key Factors to Consider when Solving Quadratic Equations
Summary 1:
169
1. The factoring method works only when the polynomial, written in
standard form is factorable.
2. Completing the square works for any quadratic equation. It can often lead to
cumbersome fractions and is usually used only when the directions specifically
request this method. It is considered an important skill
because it is
used in other situations in algebra.
3. The quadratic formula works for any quadratic equation. It is used when it
has been determined that the polynomial in the standard form equation is
not factorable or appears to be difficult to factor.
Warm-up 1. Set up and write an algebraic equation, then solve using any
appropriate method:
a) Find two consecutive even whole numbers such that the sum of their
squares is 1252.
Let x = first of two consecutive even whole numbers
_____ = second of two consecutive even whole numbers
(
)2 + ( )2
x + _____ + 4x + _____
_____ + 4x + 4
2x2 + 4x - _____
2(
)
2
x + 2x - 624
x2 + 2x
2
x + 2x + _____
2
170
= 1252
= 1252
= 1252
=0
=0
=0
= 624
= 624 + _____
(x + 1)2 = _____
x + 1=  625
x = -1 ± 25
x = _____
x + 2 = _____
or
x = _____
The two consecutive even whole numbers are _____ and _____.
Worksheet 42 (7.5)
b) The length of a rectangular plot of ground is three more than twice
its width. It is surrounded by a sidewalk of uniform width of 3
meters. Find the dimensions of the plot of ground if the area
including the sidewalk is 819 square meters.
Let
x = width of rectangular plot of ground
_______ = length of rectangular plot of ground
_______ = width of rectangle including sidewalk
_______ = length of rectangle including sidewalk
Note: Drawing a figure is helpful in this word problem.
(
2
2 x +(
)(
)
)+(
)
= 819
= 819
2 x2 + 21x - 765
x=
x=
-b 
-(
=0
2
b - 4ac
2a
)
( )2 - 4(
2( )
)(
)
- 21 
4
- 21  81
x=
4
102
60
x= or x =
4
4
x = _____ ; 2x + 3 = _____
The dimensions are ________ by ________.
x=
171
Worksheet 42 (7.5)
Problems - Set up and write an algebraic equation, then solve:
n(n - 3)
yields the number of diagonals, D, in a polygon of n
2
sides. Find the number of sides of a polygon that has 35 diagonals.
1. The formula D =
2. At a point 8 yards from the base of a tower, the distance to the top of the tower
is 2 yards more than the height of the tower. Find the height of the tower.
172
Worksheet 43 (7.6)
7.6 Quadratic Inequalities
Summary 1:
Quadratic inequalities in one variable are expressed in one of the following
forms:
173
1. ax2 + bx + c > 0
2. ax2 + bx + c  0
3. ax2 + bx + c < 0
4. ax2 + bx + c  0
A critical number in a quadratic inequality is a number that makes the given
polynomial equal to zero. It is used to help determine those values that
make the inequality true.
Finding the critical numbers on a number line for a quadratic
inequality:
1. Set ax2 + bx + c = 0 and solve for x by factoring.
2. The critical numbers are located on a number line to prepare for
graphing.
Finding the solution of a quadratic inequality using a number line
analysis:
1. Express the inequality in standard form.
2. Determine the critical numbers.
3. Organize a chart to determine appropriate intervals found by
locating critical numbers on a number line.
4. Choose one test number from within each interval and see how
it affects the sign of each factor. Use multiplication sign
rules to determine whether or not the standard form
inequality tests true.
Note: A positive product is always > 0.
A negative product is always < 0.
5. Shade intervals that test true.
6. Use ( or ) for those critical numbers that are excluded from the
solution: ax2 + bx + c > 0 or ax2 + bx + c < 0.
Use [ or ] for those critical numbers that are included in the
solution: ax2 + bx + c  0 or ax2 + bx + c  0.
7. Use set builder notation and/or interval notation to express the
solution.
Worksheet 43 (7.6)
Warm-up 1. Solve:
a)
x2 - x - 12 > 0
(x - 4)(x + 3) > 0
174
Determine critical numbers:
(x - 4)(x + 3) = 0
x = ______ or x = ______
Organize a chart for number line analysis:
(x - 4)(x + 3)=0
(x - 4)(x + 3)=0
|
|
-4
|
0
|
5
|
|
<--------------(-3)--------------(4)--------------->
(x - 4) is (-)
| (x - 4) is (-)
| (x - 4) is (+)
(x + 3) is (-)
| (x + 3) is (+)
| (x + 3) is (+)
|
|
Their product
| Their product | Their product
is positive.
is negative.
( > 0)
test values
number line
sign of product
is positive.
( < 0)
( > 0)
Graph results on a number line:
x2 - x - 12 > 0
(x - 4)(x + 3) > 0
<-------------------------------->
-3
4
Set builder notation:_______________
b) y2 - 6y + 5  0
(y - 5)(y - 1)  0
Determine critical numbers:
(y - 5)(y - 1) = 0
y = ______ or y = ______
Worksheet 43 (7.6)
Organize a chart for number line analysis:
(y - 5)(y - 1)=0
(y - 5)(y - 1)=0
|
|
175
Interval notation:__________
0
|
2
|
6
|
|
<---------------(1)--------------(5)--------------->
(y - 5) is (-)
| (y - 5) is (-)
| (y - 5) is (+)
(y - 1) is (-)
| (y - 1) is (+)
| (y - 1) is (+)
|
|
Their product
| Their product | Their product
is positive.
( > 0)
is negative.
test values
number line
sign of product
is positive.
( < 0)
( > 0)
Graph results on a number line:
y2 - 6y + 5  0
(y - 5)(y - 1)  0
<-------------------------------->
1
5
Set builder notation:_______________
Interval notation:__________
Problems - Solve:
1. x2 + x - 12  0
2. y2 + 6y + 5 < 0
Worksheet 43 (7.6)
Summary 2:
176
Rational inequalities
in one variable can be
1. xx ++ ba > 0 that are indicated
2. xx ++ ba quotients
0
solved3.using
x + a a number line analysis
4. xx ++ ba  0when expressed in one of the
x+b < 0
following forms:
The inequalities in one of the above forms have critical numbers which are
determined in each of the following ways:
1. Critical numbers determined by setting the numerator equal to zero.
These are numbers that make the quotient = 0.
2. Critical numbers determined by setting the denominator equal to
zero. These are numbers that make the quotient undefined.
Finding the solution of a rational inequality using a number line
analysis:
1. Express the inequality in one of the above forms.
Note: Use LCD to add or subtract rational expressions as one
indicated quotient.
2. Determine the critical numbers.
3. Organize a chart to determine appropriate intervals found by locating
the critical numbers on a number line graph.
4. Choose a test number in each interval and see how it affects the sign
of the factor in the numerator and the sign of the factor in the
denominator. Use division sign rules to determine whether or not
the indicated quotient in one of the above forms tests true.
Note: A positive quotient is always > 0.
A negative quotient is always < 0.
5. Shade intervals that test true.
6. Use ( or ) for those critical numbers that are excluded from the
solution: xx ++ ba > 0 , xx ++ ba < 0 ,and critical numbers that make
the
quotient undefined.
Use [ or ] for those critical numbers that are included in the solution:
x+a
x+a
x + b  0 or x + b  0
7. Use set builder notation and/or interval notation to express the
solution when directed to do so.
Worksheet 43 (7.6)
Warm-up 2. Solve:
177
a)
x -1
<0
x+5
Determine critical numbers
x-1=0
x+5=0
x = ______ x = ______
Organize a chart for number line analysis
x -1
x+5
undefined
=0
|
|
|
0
|
2
|
|
<--------------(-5)--------------(1)--------------->
(x - 1) is (-)
| (x - 1) is (-)
| (x - 1) is (+)
(x + 5) is (-)
| (x + 5) is (+)
| (x + 5) is (+)
|
|
The quotient
| The quotient
| The quotient
-6
is positive.
is negative.
( > 0)
test values
number line
sign of quotient
is positive.
( < 0)
( > 0)
Graph results on a number line
x -1
<0
x+5
<-------------------------------->
-5
1
Set builder notation:_____________ Interval notation:_________
2x + 10
1
x+4
2x + 10
-1
x+4
b)
Worksheet 43 (7.6)
2x + 10 (
x+4 (
2x + 10 - ( ) - (
x+4
)
0
)
)
0
(
)
x+4
0
178
Determine critical numbers
x+6=0
x+4=0
x = ______ x = ______
Organize a chart for number line analysis
x+6
x+4
undefined
=0
|
|
-7
|
-5
|
0
|
|
<--------------(-6)-------------(-4)--------------->
(x + 6) is (-)
| (x + 6) is (+)
| (x + 6) is (+)
(x + 4) is (-)
| (x + 4) is (-)
| (x + 4) is (+)
|
|
The quotient
| The quotient
| The quotient
is positive.
( > 0)
is negative.
test values
number line
sign of quotient
is positive.
( < 0)
( > 0)
Graph results on a number line
2x + 10
1
x+4
x+6
0
x+4
<-------------------------------->
-6
-4
Set builder notation:_____________ Interval notation:_________
Worksheet 43 (7.6)
Problems - Solve:
3.
x+3
0
x-2
179
4.
x -1
+ 1< 0
x-2
180