Download Chapter Three 3.2

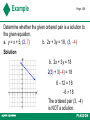
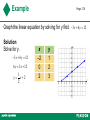
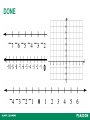
Section 3.2
Linear Equations
in Two Variables
Copyright © 2013 Pearson Education, Inc.
Example
Page 169
Determine whether the given ordered pair is a solution to
the given equation.
a. y = x + 5, (2, 7)
b. 2x + 3y = 18, (3, 4)
Solution
a.
y=x+5
7=2+5
7 = 7 True
The ordered pair (2, 7)
is a solution.
Example
Page 169
Determine whether the given ordered pair is a solution to
the given equation.
a. y = x + 5, (2, 7)
b. 2x + 3y = 18, (3, 4)
Solution
b. 2x + 3y = 18
2(3) + 3(4) = 18
6  12 = 18
6  18
The ordered pair (3, 4)
is NOT a solution.
Example
Page 170
A table can be used to list solutions to an equation.
Complete the table for the equation y = 3x – 1.
x
y
3 1 0
10
4
1
3
8
Solution
x  3
x  1
x0
x 3
y  3x  1
y  3( 3)  1
y  9  1
y  3x  1
y  3( 1)  1
y  3  1
y  3x  1
y  3x  1
y  3(0)  1
y  0 1
y  3(3)  1
y  9 1
y  10
y  4
y  1
y 8
Finding Solutions of an Equation
Page 170
A table that lists a few solutions is helpful when graphing an equation
y = 3x + 2.
Find five solutions to the equation
Choose some x values and then compute the
corresponding y values and complete the table.
X
Y
(x,y)
If x = -2,
y = 3(-2) + 2 = -4.
Ordered pair
-2
 4 (2,4)
If x = -1,
y = 3(-1) + 2 = -1.
Ordered pair
-1
 1 (1,1)
If x =0,
y = 3(0) + 2 = 2.
Ordered pair
0
2
(0,2)
If x =1,
y = 3(1) + 2 = 5.
Ordered pair
1
5
(1,5)
If x =2,
y = 3(2) + 2 = 8.
Ordered pair
2
8
( 2,8)
Graph on next slide.
Graph of the Equation
Plot the five ordered pairs to obtain the graph of y = 3x + 2
X
Y
(X,Y)
-2
-4
(-2,-4)
-1
-1
(-1,-1)
0
2
(0,2)
1
5
(1,5)
2
8
(2,8)
Example
Page 171
Make a table of values for the equation y = 3x, and then
use the table to graph this equation.
Solution
Start by selecting a few convenient values for x such
as –1, 0, 1, and 2. Then complete
the table.
x
y
–1
–3
0
0
1
3
2
6
Plot the points and connect the points
with a straight line.
Linear Equation in Two Variables
Page 172
A linear equation in two variables can be written as
Ax + By = C,
where A, B, and C are fixed numbers (constants) and A
and B are not both equal to 0.
The graph of a linear equation in two variables is a line.
Example
Graph the linear equation. y  1 x  1
4
Solution
Because this equation can be written in standard form, it is a linear equation.
Choose any three values for x.
x
–4
y
0
0
4
1
2
Plot the points and connect the points with a straight line.
Page 173
Example
Page 173
Graph the linear equation. x  y  5
Solution
Because this equation can be written in standard form, it is a linear equation.
Choose any three values for x.
x
0
2
5
y
5
3
0
Plot the points and connect the points with a straight line.
Example
Page 174
Graph the linear equation by solving for y first. 3x  6 y  12
Solution
Solve for y.
3 x  6 y  12
6 y  3 x  12
1
y  x2
2
x
–2
0
2
y
1
2
3
Graph of the Equation
Plot the five ordered pairs to obtain the graph of y = 3x + 1
(2,7)
(1,4)
(0,1)
(-1,-2)
(-2,-5)
X
Y
(x,y)
2
7
(2,7)
1
4
(1,4)
0
1
(0,1)
-1
-2
(-1,-2)
-2
-5
(-2,-5)
DONE
Tables of Solutions
Page 170
A table can be used to list solutions to an equation.
A table that lists a few solutions is helpful when graphing
an equation.
Basic Concepts
Page 168
Equations can have any number of variables.
A solution to an equation with one variable is one number
that makes the statement true.
Page 172
Example
Page 174
Graph the linear equation by solving for y first. 3x  6 y  12
Solution
Solve for y.
3 x  6 y  12
6 y  3 x  12
1
y  x2
2
x
–2
0
2
y
1
2
3
Graph of the Equation
Plot the ordered pairs to obtain the graph of y = 2x
y  2(1)
y2
y  2  (0)
y0
y  2  (2)
y4
y  2  (2)
y  4
Graph of the Equation
Plot the ordered pairs to obtain the graph of y = 2x-2
y  2(1)  2
y0
y  2  ( 0)  2
y  2
y  2  ( 2)  2
y2
y  2  (2)  2
y  6
Graph of the Equation
Plot the ordered pairs to obtain the graph of
1
y  x2
2
1
( 2)  2
2
y3
y
1
 (0)  2
2
y2
y
1
 (4)  2
2
y4
y
1
 ( 2)  2
2
y 1
y
Graph of the Equation
Plot the five ordered pairs to obtain the graph of y = 3x + 2
X
Y
(x,y)
-2
-4
(-2,-4)
-1
-1
(-1,-1)
0
2
(0,2)
1
5
(1,5)
2
8
(2,8)