* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download joint and conditional distributions
Survey
Document related concepts
Transcript
PROBABILITY AND BAYES
THEOREM
1
PROBABILITY
SAMPLE
POPULATION
STATISTICAL
INFERENCE
2
• PROBABILITY: A numerical value expressing
the degree of uncertainty regarding the
occurrence of an event. A measure of
uncertainty.
• STATISTICAL INFERENCE: The science of
drawing inferences about the population
based only on a part of the population,
sample.
3
PROBABILITY
• CLASSICAL INTERPRETATION
If a random experiment is repeated an infinite number of
times, the relative frequency for any given outcome is the
probability of this outcome.
Probability of an event: Relative frequency of the
occurrence of the event in the long run.
– Example: Probability of observing a head in a fair coin toss is 0.5 (if coin is tossed
long enough).
• SUBJECTIVE INTERPRETATION
The assignment of probabilities to event of interest is
subjective
– Example: I am guessing there is 50% chance of raining today.
4
PROBABILITY
• Random experiment
– a random experiment is a process or course of action, whose
outcome is uncertain.
• Examples
Experiment
• Flip a coin
• Record a statistics test marks
• Measure the time to assemble
a computer
Outcomes
Heads and Tails
Numbers between 0 and 100
Numbers from zero and above
5
PROBABILITY
• Performing the same random experiment
repeatedly, may result in different outcomes,
therefore, the best we can do is consider the
probability of occurrence of a certain
outcome.
• To determine the probabilities, first we need
to define and list the possible outcomes
6
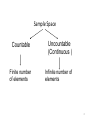
Sample Space
• Determining the outcomes.
– Build an exhaustive list of all possible outcomes.
– Make sure the listed outcomes are mutually
exclusive.
• The set of all possible outcomes of an
experiment is called a sample space and
denoted by S.
7
Sample Space
Countable
Uncountable
(Continuous )
Finite number
of elements
Infinite number of
elements
8
EXAMPLES
• Countable sample space examples:
– Tossing a coin experiment
S : {Head, Tail}
– Rolling a dice experiment
S : {1, 2, 3, 4, 5, 6}
– Determination of the sex of a newborn child
S : {girl, boy}
• Uncountable sample space examples:
– Life time of a light bulb
S : [0, ∞)
– Closing daily prices of a stock
S : [0, ∞)
9
EXAMPLES
• Examine 3 fuses in sequence and note the
results of each experiment, then an outcome
for the entire experiment is any sequence of
N’s (non-defectives) and D’s (defectives) of
length 3. Hence, the sample space is
S : { NNN, NND, NDN, DNN, NDD,
DND, DDN, DDD}
10
Assigning Probabilities
– Given a sample space S ={O1,O2,…,Ok}, the following
characteristics for the probability P(Oi) of the simple
event Oi must hold:
1.
0 POi 1 for each i
k
2.
PO 1
i
i 1
– Probability of an event: The probability P(A), of
event A is the sum of the probabilities assigned to
the simple events contained in A.
11
Assigning Probabilities
• P(A) is the proportion of times the event A is
observed.
total outcomes in A
P( A)
total outcomes in S
12
Intersection
• The intersection of event A and B is the event that
occurs when both A and B occur.
• The intersection of events A and B is denoted by (A
and B) or AB.
• The joint probability of A and B is the probability of
the intersection of A and B, which is denoted by P(A
and B) or P(AB).
13
Union
• The union event of A and B is the event that
occurs when either A or B or both occur.
• At least one of the events occur.
• It is denoted “A or B” OR AB
14
Complement Rule
• The complement of event A (denoted by AC) is
the event that occurs when event A does not
occur.
• The probability of the complement event is
calculated by
A and AC consist of all the
simple events in the
sample space. Therefore,
P(A) + P(AC) = 1
P(AC) = 1 - P(A)
15
MUTUALLY EXCLUSIVE EVENTS
• Two events A and B are said to be mutually
exclusive or disjoint, if A and B have no
common outcomes. That is,
A and B = (empty set)
•The events A1,A2,… are pairwise mutually
exclusive (disjoint), if
Ai Aj = for all i j.
16
EXAMPLE
• The number of spots turning up when a sixsided dice is tossed is observed. Consider the
following events.
A: The number observed is at most 2.
B: The number observed is an even number.
C: The number 4 turns up.
17
VENN DIAGRAM
• A graphical representation of the sample
1
space.
A
AB
S
1
2
B
4
A
3
6
5
C
4
2
1
B
6
AB
A
22
4
AC = A and C are mutually exclusive
B
6
18
AXIOMS OF PROBABILTY
(KOLMOGOROV AXIOMS)
Given a sample space S, the probability function
is a function P that satisfies
1) For any event A, 0 P(A) 1.
2) P(S) = 1.
3) If A1, A2,… are pairwise disjoint, then
P
n
i 1
Ai
P( A ), n 1,2,...
i
i 1
19
THE CALCULUS OF PROBABILITIES
•
If P is a probability function and A is any set,
then
a. P()=0
b. P(A) 1
c. P(AC)=1 P(A)
20
THE CALCULUS OF PROBABILITIES
•
If P is a probability function and A and B any
sets, then
a. P(B AC) = P(B)P(A B)
b. If A B, then P(A) P(B)
c. P(A B) P(A)+P(B) 1 (Bonferroni Inequality)
d. P
i 1
Ai
P A for any sets A , A ,
i
1
2
i 1
(Boole’s Inequality)
21
EQUALLY LIKELY OUTCOMES
• The same probability is assigned to each simple
event in the sample space, S.
• Suppose that S={s1,…,sN} is a finite sample space. If
all the outcomes are equally likely, then P({si})=1/N
for every outcome si.
22
Addition Rule
For any two events A and B
P(A B) = P(A) + P(B) - P(A B)
23
ODDS
• The odds of an event A is defined by
P( A)
P( A)
C
P( A ) 1 P( A)
•It tells us how much more likely to see the
occurrence of event A.
•P(A)=3/4P(AC)=1/4 P(A)/P(AC) = 3.
That is, the odds is 3. It is 3 times more
likely that A occurs as it is that it does not.
24
CONDITIONAL PROBABILITY
• (Marginal) Probability: P(A): How likely is it
that an event A will occur when an experiment
is performed?
• Conditional Probability: P(A|B): How will the
probability of event A be affected by the
knowledge of the occurrence or
nonoccurrence of event B?
• If two events are independent, then
P(A|B)=P(A)
25
CONDITIONAL PROBABILITY
P(A B)
P(A | B)
if
P(B)
0 P(A | B) 1
P(B) 0
P(A | B) 1 P(A C | B)
P(A | A) 1
P(A1 A 2 | B) P(A1 | B) P(A 2 | B) P(A1 A 2 | B)
26
Example
•
•
•
•
Roll two dice
S=all possible pairs ={(1,1),(1,2),…,(6,6)}
Let A=first roll is 1; B=sum is 7; C=sum is 8
P(A|B)=?; P(A|C)=?
• Solution:
• P(A|B)=P(A and B)/P(B)
P(B)=P({1,6} or {2,5} or {3,4} or {4,3} or {5,2} or {6,1})
= 6/36=1/6
P(A|B)= P({1,6})/(1/6)=1/6 =P(A)
A and B are
independent
27
Example
• P(A|C)=P(A and C)/P(C)=P(Ø)/P(C)=0
A and C are disjoint
Out of curiosity:
P(C)=P({2,6} or {3,5} or {4,4} or {5,3} or {6,2})
= 5/36
BAYES THEOREM
• Suppose you have P(B|A), but need P(A|B).
P(A B) P(B | A)P(A)
P(A | B)
for P(B) 0
P(B)
P(B)
• Can be generalized to more than two events.
29
Example
• Let:
– D: Event that person has the disease;
– T: Event that medical test results positive
• Given:
– Previous research shows that 0.3 % of all Turkish population
carries this disease; i.e., P(D)= 0.3 % = 0.003
– Probability of observing a positive test result for someone with
the disease is 95%; i.e., P(T|D)=0.95
– Probability of observing a positive test result for someone
without the disease is 4%; i.e. P(T|
)=C0.04
D
• Find: probability of a randomly chosen person having the disease
given that the test result is positive.
30
Example
• Solution: Need P(D|T). Use Bayes Thm.
P(D|T)=P(T|D)*P(D)/P(T)
P(T)=P(D and T)+P( D C and T)
= 0.95*0.003+0.04*0.997 = 0.04273
P(D|T) =0.95*0.003 / 0.04273 = 6.67 %
Test is not very reliable!
31