* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Notes 5.6
Survey
Document related concepts
Transcript
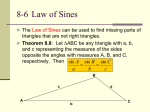
Section 5.6 The Law of Sines Objective: Students will be able to: 1. Solve triangles using the Law of Sines if the measures of 2 angles and a side are given. 2. Find the area of a triangle if the measures of 2 sides and the included angle or the measures of 2 angles and a side are given. Law of Sines The ___________________ can be used to solve triangles that are not right triangles. Law of Sines Let ∆𝐴𝐵𝐶 be any triangle with a, b and c representing the measures of the sides opposite the angles with measures A, B, and C respectively. Then, the following is true: 𝑎 𝑏 𝑐 = = sin 𝐴 sin 𝐵 sin 𝐶 From geometry, you know that a unique triangle can be formed if you know the measures of 2 angles and the included side (ASA) or the measures of 2 angles and the non-included side (AAS). Therefore, there is one unique solution when you use the Law of Sines to solve a triangle given the measures of 2 angles and one side. *** In Section 5.7, you will learn how to use the Law of Sines when the measures of 2 sides and a nonincluded angle are given. Example 1: Solve ABC if A = 24°, B = 62°, and a = 21.4. First, find the measure of C. C = 180° - (24° + 62°) or 94° Use the Law of Sines to find b and c. Find b : 𝑎 sin 𝐴 𝑏 = sin 𝐵 Find c : 𝑐 sin 𝐶 = 𝑎 sin 𝐴 21.4 𝑏 = sin 24° sin 62° 𝑐 21.4 = sin 94° sin 24° 21.4 sin 62° =𝑏 sin 24° 𝑐= 46.45531404 𝑏 ≈ 46.5 b 21.4 sin 94° sin 24° 52.48573257 𝑐 ≈ 52.5 c Example 2: The angle of depression from a window of a house to the front edge of the swimming pool is 26.6°. The angle of depression from this same window to the back edge of the swimming pool is 15.3°. The length of the pool is 25 feet. If a person looks out the window, about how far is he from the front edge of the pool? *** Make a diagram of the problem. Remember that the angle of elevation is congruent to the angle of depression because they are alternate interior angles. First, find . = 26.6° - 15.3° or 11.3° Use the Law of Sines to find d. 𝑑 25 = sin 15.3° sin 11.3° 25 sin 15.3° 𝑑= sin 11.3° d 33.66652748 The person would be about 33.7 feet from the front edge of the pool. The area of any triangle can be expressed in terms of 2 sides of a triangle and the measure of the included angle. Area of Triangles Let ∆ 𝐴𝐵𝐶 be any triangle with a, b, and c representing the measures of the sides opposite the angles with measurements A, B, and C, respectively. Then the area K can be determined using one of the following formulas: 𝐾= 1 𝑏𝑐 sin 𝐴 2 , 𝐾= 1 𝑎𝑐 sin 𝐵 2 , 𝐾= Example 3: Find the area of ABC if b = 14.8, c = 10.2, and A = 54°12. 1 K = 𝑏𝑐 sin 𝐴 2 1 2 𝐾 = (14.8)(10.2) sin (54° 12′ ) K 61.21909706 The area of ABC is about 61.2 square units. 1 𝑎𝑏 sin 𝐶 2 You can also find the area of a triangle if you know the measures of one side and 2 𝑏 𝑐 𝑐 sin 𝐵 angles of the triangle. By the Laws of Sines , sin 𝐵 = sin 𝐶 𝑜𝑟 𝑏 = sin 𝐶 , if you substitute 𝑐 sin 𝐵 sin 𝐶 1 𝟏 for b in K = 2 𝑏𝑐 sin 𝐴, the result is K = 𝟐 𝒄𝟐 𝐬𝐢𝐧 𝑨 𝐬𝐢𝐧 𝑩 𝐬𝐢𝐧 𝑪 . Two similar formulas can be developed from the Laws of Sines: 𝟏 𝑲 = 𝟐 𝒂𝟐 𝐬𝐢𝐧 𝑩 𝐬𝐢𝐧 𝑪 𝐬𝐢𝐧 𝑨 and 𝟏 𝑲 = 𝟐 𝒃𝟐 𝒔𝒊𝒏 𝑨 𝒔𝒊𝒏 𝑪 𝒔𝒊𝒏 𝑩 Example 4: Find the area of DEF if e = 18.6, E = 78.2°, and F = 41.3°. First find the measure of D. D = 180° - (78.2° + 41.3°) or Then, find the area of the triangle. 1 sin 𝐷 sin 𝐹 K = 𝑒2 2 sin 𝐸 1 sin 60.5° sin 41.3° 𝐾 = (18.6)2 2 sin 78.2° 60.5° K 101.5111719 The area of DEF is about 101.5 square units.