* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download A Statistical Method for Finding Transcriptional Factor Binding Sites
Multi-state modeling of biomolecules wikipedia , lookup
Genome evolution wikipedia , lookup
Gene expression profiling wikipedia , lookup
Cre-Lox recombination wikipedia , lookup
Molecular evolution wikipedia , lookup
Gene regulatory network wikipedia , lookup
Non-coding DNA wikipedia , lookup
Community fingerprinting wikipedia , lookup
Transcriptional regulation wikipedia , lookup
Ligand binding assay wikipedia , lookup
Silencer (genetics) wikipedia , lookup
Endogenous retrovirus wikipedia , lookup
Promoter (genetics) wikipedia , lookup
Cooperative binding wikipedia , lookup
A Statistical Method for Finding
Transcriptional Factor Binding Sites
Authors: Saurabh Sinha and Martin Tompa
Presenter: Christopher Schlosberg
CS598ss
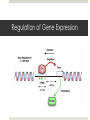
Regulation of Gene Expression
Difficulties of Motif Finding
Regulatory sequences don’t follow same
orientation as the coding sequence or each
other
Multiple binding sites might exist for each
regulated gene
Large variation in the binding sites of a single
factor. Variations are not well understood.
Previous & Proposed Methods for
Finding Motifs
Previous Methods:
Find longer, general motifs
Use local search algorithms (Gibbs sampling,
Expectation Maximization, greedy algorithms)
Proposed Method:
TFBS is small enough to use enumerative methods
Enumerative statistical methods guarantee global
optimality and affordability
Proposed Method Highlights
Allows variations in the binding site instances of a given transcription
factor
Allows for motifs to include “spacers”
Allows for overlapping occurrences (in both orientations), which
lends to complex dependencies
Statistical significance of a motif (s) is based on the frequencies of
shorter (more frequent) oligonucleotides
Use of Markov chain to model background genomic distribution
Use of z-score to measure statistical significance
Allows for multiple binding sites
Characteristics of a Motif
Any single TFBS has significant variation
Many motifs have spacers from 1-11bp
Variation often occurs as a transition (e.g. purine
purine) rather than a transversion (e.g. pyrimidine
purine)
Variation occurs less between a pair of complementary
bases.
Indels are uncommon
Proposed Motif Definition
Motif will be a string with Σ= {A,C,G,T, R,Y,S,W,N}
A,C,G,T (DNA bp), R (purine), Y (pyrimidine), S (strong), W
(weak), N (spacer)
TF database (SCPD) confirms this model of variation
Of 50 binding site consensi, 31 exact fits (62%)
Another 10 fit if slight variations allowed
Measure of Statistical Significance
Given set of corregulated S. cerevisiae genes, the input to the
problem is corresponding set of 800bp upstream sequences having
3’ end on start site of gene translation.
Model must measure from input sequences:
Absolute number of occurrences (Ns) of motif (s)
Background genomic distribution
X is a set of random DNA sequences in the same number and
lengths of the input sequences
Generated by Markov chain of order m
Transition probabilities determined by (m+1)-mer frequencies in fully
complement of 6000+ (800bp in length)
Background model chooses m=3
z-score
Xs – r.v. is number of occurrences of motif (s) in X
E(Xs) – expectation, σ(Xs) – standard deviation
zs – number of S.D. by which observed value Ns exceeds
expectation
Implications
Possibility of overlap of a motif with itself (in either
orientation)
Previous study of pattern autocorrelation
Generalized computation of SD, treating motif as a finite
set of strings
Higher order Markov chains
Spacers handled at no extra computational cost
Handles motif in either orientation
Algorithm
Enumerates over each input sequence
Tabulates number Ns of occurrences of each motif in
either direction
Compute expectation and SD for each motif s.t. Ns>0
Calculate z-score
Rank motifs by z-score
Algorithm Analysis
For single motif, complexity is O(c2k2)
k – # of nonspacer characters in motif
c – # of instantiations of R, Y, S, W in motif
Only modest values of k
Linear dependence on genome size
Can trim variance calculation to optimize
Number of Occurrences
Convert motif s into a multiset W
Add reverse complements for each string in W
Motif s only occurs at position in X iff some string in W occurs
at same position
Xs - # of occurrences (in X) of each member of W
Handling Palindromes
Wi – member of W
|W| = T
Number of Occurrences Con’t
Expectation
Linearity of Expectation
Variance
B term
C term
C Term
A term
A Term
Overlapping Concatenation
CW (like W) is potentially a multiset
One-to-one correspondence
C Term Simplification
A Term Revisited
Si1Si2 Term & Approximation
Kleffe and Borodovsky (1992) Approximation
B Term
B Term Con’t
Summary
Higher Order Markov Models
Variance calculations remain the same except for Si1Si2
term
Experimental m = 3
Experimental Results & Future
Considerations
17 coregulated sets of genes
Known TF with known binding site consensus
In 9 experiments, known consensus was one of 3 highest
scoring motifs
Future Topics:
Non-centered spacers
Enumeration Loop optimization
Filtering repeats
Question
E(Xs) is more straight-forward to calculate
compared to σ(Xs). Under the assumptions
given in the paper, name one of the reasons for
this complication.