Download Chapter 6 – Work and Energy

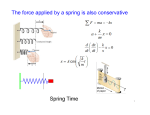
Chapter 6 – Work and Energy
Old assignments and midterm exams
(solutions have been posted on
the web)
can be picked up in my office
(LB-212)
Assignment 7
Textbook (Giancoli, 6th edition), Chapter 6-7:
Due on Thursday, November 6, 2008
- Problem 37 - page 163 of the textbook
- Problem 69 - page 165 of the textbook
- Problems 14 and 15 - page 188 of the textbook
All marks, including assignments, have
been posted on the web.
http://ilc2.phys.uregina.ca/~barbi/academic/phys109/marks.pdf
Please, verify that all your marks have
been entered in the list.
Chapter 6
• Work Done by a Constant Force
• Kinetic Energy, and the Work-Energy Principle
• Potential Energy
• Conservative and Nonconservative Forces
• Mechanical Energy and Its Conservation.
Recalling Last Lecture
Potential Energy
Potential energy is the ability of an object to
do work.
Gravitational potential energy is
(6-9)
(6-10)
Potential Energy
The force needed to compress or stretch a string is written as:
Where,
k = spring stiffness constant
Newton’s 3rd law says that the spring will
exert a force FS in reaction to the force
FP such that:
(6-11)
Eq. 6.11 (spring equation) is known as Hooke’s law
FS is the force the spring exerts opposite to
its displacement in an attempt to restore its original length
Potential Energy
Elastic potential energy is:
(6-12)
Conservative and Nonconservative Forces
When the work done by a force does NOT depend on the path taken, this FORCE is
said to be CONSERVATIVE.
Example:
1) Gravitational force: F = mg;
2) Elastic force: F = -kx;
W = mgh
(h = vertical displacement)
W = ½ kx2
Note: If an object starts at a given point and returns to the same point, the net
work done is ZERO if the forces acting on it are conservative.
Example:
You lift an object by a vertical displacemen h: W1 = mgh
You move the same back to its original position: W2 = mg(-h) = -mgh
Net work done on the object: Wnet = W1 + W2 = mgh + (-mgh) = 0
Conservative and Nonconservative Forces
When the work done by a force DOES depend on the path taken, this FORCE is
said to be NONCONSERVATIVE.
Example:
Friction forces the work done depends not only on the starting and
ending points, but also on the path taken
In general, forces that change as the direction of displacement changes are
nonconservatives.
Conservative and Nonconservative Forces
We have seen that the potential energy associated to a force is the energy stored at
some point. Gravitational potential energy is an example.
This only makes sense if this energy can be defined uniquely for a given point
(otherwise you would have two potential energies associate to a force at the same
point two different abilities of an object at that particular point to do work -- > this
cannot be!)
However, we just stated that the work done by NONCONSERVATIVE forces do
depend on the path taken
It does NOT make sense to define potential energy associate to non-conservative
forces as you would have more then one at a given point
Nonconservative forces do NOT have a potential energy associated to them.
Thus, potential energy can be defined only for conservative forces.
Conservative and Nonconservative Forces
General form of the work-energy principle
Observing the two previous slides, we can now generalize the work-energy principle
to include the potential energy.
Recalling: We previously wrote Wnet = ∆KE
Now consider an object subject to both nonconservative and conservative forces. The
net work done is:
Where,
Conservative and Nonconservative Forces
General form of the work-energy principle
Observing the two previous slides, we can now generalize the work-energy principle
to include the potential energy.
Recalling: We previously wrote Wnet = ∆KE
Now consider an object subject to both nonconservative and conservative forces. The
net work done is:
Where,
Conservative and Nonconservative Forces
General form of the work-energy principle
But, from the work-energy principle, we know that:
(6-13)
We have also seen that the work done by a conservative force, WC , can be written in
terms of the potential energy:
We can then rewrite eq. 6-13 as:
(6-14)
Eq. 6-14 tells us that the work done by nonservative forces is equal to the total
change in kinetic and potential energies.
Conservative and Nonconservative Forces
Dissipative energy
The work done by nonconservative force is NOT used to move an object
The energy used to do this work is dissipated it will change the total
mechanical energy in the system.
Nonconservative forces are also known as DISSIPATIVE FORCES.
Example: When I push my finger on a surface, the initial mechanical energy in my
fingers is the sum of the potential and kinetic energies.
But then friction acts against my finger’s motion.
The work done my the friction force is not used to move your fingers.
Instead, it tries to slow it down by dissipating part of the total energy available
This energy is dissipated in form thermal energy (heat) you can feel your
fingers getting warmer
Mechanical Energy and its Conservation
If ONLY conservatives forces are present, eq. 6.14 can be written as
or
(6-15)
We can now define the total mechanical energy stored on a object at certain instant
of time as:
(6-16)
And then rewrite eq. 6-15, yielding the equation of conservation of energy:
(6-17)
Mechanical Energy and its Conservation
Eq. 6.17 states the following:
“ If only conservative forces are acting, the TOTAL MECHANICAL ENERGY of a
system neither increases nor decreases in any process. It stays constant it
is CONSERVED”
POWER:
Power is the rate at which work is done, or the rate at which energy is
transformed.
(6-18)
In the SI system the unit of power is:
In general, if an object moves with average velocity
1 hp = 746 W
, the power can be written as
(6-19)
Kinetic Energy, and the Work Energy Principle
Problem 6-36 (textbook): In the high jump, Fran’s kinetic energy is transformed into
gravitational potential energy without the aid of a pole. With what minimum speed
must Fran leave the ground in order to lift her center of mass 2.10 m and cross the
bar with a speed of 0.70 m/s ?
Kinetic Energy, and the Work Energy Principle
Problem 6-36:
We assume that all the forces on the jumper are conservative, so that the mechanical
energy of the jumper is conserved.
Subscript 1 represents the jumper at the bottom of the jump, and subscript 2
represents the jumper at the top of the jump.
Call the ground the zero location for PE ( y = 0). We have:
y1 = 0
y 2 = 2.10 m
v 2 = 0.70 m s
Solve for v1, the speed at the bottom.
1
2
m v12 + m gy1 =
v1 =
1
2
m v 22 + m gy 2
v 22 + 2 gy 2 =
→
( 0.70 m s )
2
1
2
(
m v12 + 0 =
+ 2 9.80 m s 2
1
2
m v 22 + m gy 2
) ( 2.10 m ) =
→
6.45 m s
Kinetic Energy, and the Work Energy Principle
Problem 6-76 (textbook) An airplane pilot fell 370 m after jumping from an aircraft
without his parachute opening. He landed in a snowbank, creating a crater 1.1 m
deep, but survived with only minor injuries. Assuming the pilot’s mass was 78 kg and
his terminal velocity was 35 m/s, estimate
(a) the work done by the snow in bringing him to rest;
(b) the average force exerted on him by the snow to stop him;
(c) the work done on him by air resistance as he fell.
Kinetic Energy, and the Work Energy Principle
Problem 6-76 :
(a)
Use conservation of energy, including the work done by the non-conservative force of
the snow on the pilot. Subscript 1 represents the pilot at the top of the snowbank,
and subscript 2 represents the pilot at the bottom of the crater. The bottom of the
crater is the zero location for PE ( y = 0 ) . We have
v1 = 35 m/s ,
y1 = 1.1 m,
v2 = 0,
y2 = 0
Solve for the non-conservative work:
W N C + E1 = E 2
→
W NC +
W N C = − 12 m v12 − m gy1 = −
1
2
1
2
( 78
m v12 + m gy1 =
1
2
m v 22 + m gy 2
(
→
kg )( 35 m s ) − ( 78 kg ) 9.8 m s 2
= − 4.862 × 10 4 J ≈ − 4.9 × 10 4 J
2
) (1.1 m )
Kinetic Energy, and the Work Energy Principle
Problem 6-76 :
(b)
The work done by the snowbank is done by an upward force, while the pilot moves
down.
W N C = F sn o w d c o s 1 8 0 o = − F sn o w d
Fsn o w = −
W NC
d
= −
− 4.862 × 10 4 J
1 .1 m
→
= 4.420 × 10 4 N ≈ 4.4 × 10 4 N
Kinetic Energy, and the Work Energy Principle
Problem 6-76 :
(c)
To find the work done by air friction, another non-conservative force, use energy
conservation including the work done by the non-conservative force of air friction.
Subscript 1 represents the pilot at the start of the descent, and subscript 2 represents
the pilot at the top of the snowbank. The top of the snowbank is the zero location for
PE ( y = 0 ) . We have
v1 = 0 m/s ,
y1 = 370 m,
v2 = 35 m/s,
y2 = 0.
Solve for the non-conservative work.
W NC + E1 = E 2
W NC =
1
2
→ W NC + 12 mv12 + mgy1 =
mv 22 − mgy1 =
1
2
1
2
mv 22 + mgy 2
(
→
( 78 kg )( 35 m s ) − ( 78 kg ) 9.8 m s 2
= − 2.351 × 10 5 J ≈ − 2.4 × 10 5 J
2
) ( 370 m )
Kinetic Energy, and the Work Energy Principle
Problem 6-63 (textbook): A driver notices that her 1150-kg car slows down from
85 Km/h to 65 Km/h in about 6.0 s on the level when it is in neutral. Approximately
what power (watts and hp) is needed to keep the car traveling at a constant
75 km/h?
Kinetic Energy, and the Work Energy Principle
Problem 6-63
The energy transfer from the engine must replace the lost kinetic energy. From the
two speeds, calculate the average rate of loss in kinetic energy while in neutral.
 1m s

 1m s 
=
23.61
m
s
v
=
65
km
h
= 18.06 m s
2



 3.6 km h 
 3.6 km h 
2
2
∆ KE = 12 mv 22 − 12 mv12 = 12 (1150 kg )  (18.06 m s ) − ( 23.61 m s )  = − 1.330 × 10 5 J
v1 = 85 km h 
P=
W
t
=
1.330 × 10 5 J
6.0 s
(
= 2.216 × 10 W , or 2.216 × 10 W
4
4
) 746 W = 29.71 hp
1 hp
Note now that 75 Km/h is the average between the car’s initial and final speeds:
⇒ We can use
the
2.2 × 10 4 W or 3.0 × 101 hp is needed from the engine.
to conclude