Download Section 0.2 Integer Exponents and Scientific Notation

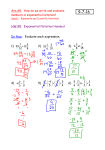
Section 0.2 Integer Exponents and
Scientific Notation
Natural-Number Exponents
When two or more quantities are multiplied together, each quantity is called a factor of the product.
For any natural mumber n, xn = x · x · x · x · · · x
• In the exponential expression xn , x is the base and n is the exponent or power to which the
base is raised. The expression xn is called a power of x. NOTE: x1 = x.
• The number 1 is not usually written.
• Ex: Write each expression without using exponents:
a. 32 = 9
b. (−3)2 = (−3)(−3) = 9
c. 2x4 = 2 · x · x · x · x
d. (2x)4 = (2x)(2x)(2x)(2x) = 16 · x · x · x · x
• NOTE: axn 6= (ax)n . axn = a · x · x · x · · · x while (ax)n = (ax)(ax)(ax) · · · (ax).
Also, −xn 6= (−x)n . −xn = −x · x · x · · · x while (−x)n = (−x)(−x)(−x) · · · (−x).
Rules of Exponents
• Product Rule for Exponents If m and n are natural numbers, xm xn = xm+n .
• NOTE: The product rule only applies to exponential expressions with the same base.
• Power Rule of Exponents If m and n are natural numbers, then
!n
xn
x
m n
mn
n
n n
= n , (y 6= 0)
(x ) = x
(xy) = x y
y
y
Ex: Simplify
a. x3 x7 = x3+7 = x10
b. x3 y 3!
x4 y 2 = x3+4 y 3+2 = x7 y 5
2
x2
x4
c.
=
y3
y6
• Zero Exponent x0 = 1, (x 6= 0).
• Negative Exponents If n is an integer and x 6= 0, then
x−n =
1
xn
1
= xn
x−n
• Quotient Rule for Exponents If m and n are integers, then
xm m−n
x
(x 6= 0)
=
• A Fraction to a Negative Power If n is a natural number, then
x
y
!−n
=
n
y
x
(x 6= 0, y 6= 0)
Ex: Simplify and write all answers without using negative exponents.
x−6
1
a. 2 = x(−6)−2 = x−8 = 8
x
x
b.
c.
x5 x−3
= x5+(−3)−2 = x0 = 1
x2
3x2 y −5
2x−2 y −6
!−3
=
3x2 x2 y 6
2y 5
!−3
=
3x4 y 6
2y 5
!−3
=
3x4 y
2
!−3
=
2
3x4 y
!3
=
8
27x12 y 3
Order of Operations
Please Excuse My Dear Aunt Sally: (Parenthesis, Exponents, Multiplication/Division, Addition/ Subtraction)
1. Work from innermost to outermost grouping symbols (parenthesis or brackets).
2. Find the values of any exponential expressions.
3. Perform all multiplication and/or division from left to right.
4. Perform all addition and/or subtraction from left to right.
5. In a fraction, simplify the numerator and denominator separately. Then simplify.
Evaluating Expressions
Ex: If x = −2, y = 0, andz = 3, evaluate the expression: 5x2 − 3y 3 z = 5(−2)2 − 3(0)3 (3) =
5(4) − 3(0)(3) = 20 − 0 = 20
Scientific Notation
• Scientific Notation A number is written in scientific notation when it is written in the form
N x10n where 1 ≤ |N | < 10 and n is an integer.
• We can write 372000 in scientific notation. To do so, we need to write it as the product
of a number between 1 and 10 and some power of 10. The number 3.72 is between 1 and
10. We can change 3.72 into 372000 by moving the decimal point 5 places to the right. So,
3.72x105 = 372000.
Using Scientific Notation to Simplify Computations
Ex: Calculate
(0.00000035)(170, 000)
using scientific notation.
0.00000085
(3.5x107)(1.70x105)
5.95
(3.5)(1.7)(107+5 )
=
=
7
7
8.5x10
(8.5)(10 )
8.5
1012
107
!
= 0.7x105 = 7x104