* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Relationships Between Lines (3.1, 3.2)
Survey
Document related concepts
Transcript
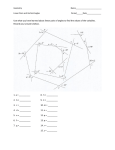
Geometry B Chapter 3 Guided Notes Name___________________________ Day One: Relationships Between Lines (3.1, 3.2) Types of Lines: • Parallel Lines: _________________________________________________________________ o Notation: __________ • Skew Lines: ___________________________________________________________________ • Perpendicular Lines: ___________________________________________________________ o • Notation: __________ Transversal: ___________________________________________________________________ Angles Formed by Transversals: 1. Corresponding Angles: _________________________________________________________ o Example: _____________________________________ 2. Alternate Exterior Angles: ______________________________________________________ o Example: _____________________________________ 3. Alternate Interior Angles: _______________________________________________________ o Example: _____________________________________ 4. Consecutive Interior Angles: ____________________________________________________ o Example: _____________________________________ Day Two: Parallel Lines & Their Angles (3.3) If two lines are parallel, then: 1. Corresponding Angles _________________________________ 2. Alternate Exterior Angles _______________________________ 3. Alternate Interior Angles ________________________________ 4. Consecutive Interior Angles _____________________________ Examples: A. If <1 = 110°, then <8 = _______ Type of angles __________________ B. If <4 = 125°, then <6 = _______ Type of angles __________________ C. If <6 = 70°, then <2 = _______ Type of angles __________________ D. If <5 = 140°, then <8 = _______ Type of angles __________________ E. If <3 = 60°, then <6 = _______ Type of angles __________________ Day Three: More with Parallel Lines (3.4, 3.5) How can we tell if two lines are parallel? Example A 1. Is line l parallel to line m? 2. Is line n parallel to line o? Example B 1. 2. Day Four: Equations of Parallel Lines (3.6) Slope = Slope-Intercept Form: Point-Slope Form: PARALLEL LINES HAVE ________________________________!! Finding Equations of Parallel Lines: Use the __________ of the original line and ________________________ to write an equation. ! Example: Write the equation for the line that is parallel to the line 𝑦 = − 𝑥 − 1 and passes ! through the point (3, 2). Day Five: Equations of Perpendicular Lines (3.7) Warm Up: Find the reciprocals of the numbers below. A. ! C. − B. 4 ! ! ! D. –2 Reciprocals: _________________________________________________________________________ PERPENDICULAR LINES HAVE _____________________________________________!! Example: Identify the slope of each line. Write the opposite sign reciprocal of that slope. ! 1. 𝑦 = 𝑥 − 1 ! ! 2. 𝑦 = − 𝑥 + 4 ! 3. 𝑦 = −3𝑥 − 5 Finding Equations of Perpendicular Lines: Use the __________________________________ of the original line and ________________________ to write an equation. ! Example 1: Write the equation for the line that is perpendicular to the line 𝑦 = − 𝑥 − 1 and ! passes through the point (3, 2). Example 2: Write the equation for the line that is perpendicular to the line 𝑦 = 2𝑥 + 4 and passes through the point (4, –3).