Fibonacci numbers at most one away from a perfect power
... [14], [15], and N. Robbins [29]. In Section 2.6 of [1], J.A. Antoniadis gave an alternative resolution of Fn − 1 = y 2 . The traditional approach to equations involving Fibonacci numbers combines clever tricks with various elementary identities connecting Fibonacci and Lucas numbers. This is the app ...
... [14], [15], and N. Robbins [29]. In Section 2.6 of [1], J.A. Antoniadis gave an alternative resolution of Fn − 1 = y 2 . The traditional approach to equations involving Fibonacci numbers combines clever tricks with various elementary identities connecting Fibonacci and Lucas numbers. This is the app ...
Presentation on Weierstrass M-Test
... Any sequence that satisfies the Cauchy Criterion is known as a Cauchy sequence. The above theorem also shows that every convergent sequence is Cauchy, and every Cauchy sequence is convergent. COROLLARY 1: If is a Cauchy sequence that converges to Z, and N is chosen such that every such that , then f ...
... Any sequence that satisfies the Cauchy Criterion is known as a Cauchy sequence. The above theorem also shows that every convergent sequence is Cauchy, and every Cauchy sequence is convergent. COROLLARY 1: If is a Cauchy sequence that converges to Z, and N is chosen such that every such that , then f ...
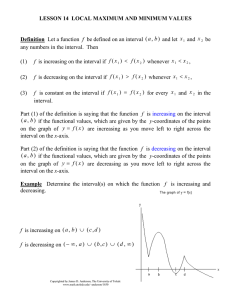
DEFINITE INTEGRALS
... shaded region in Fig.27.3. Now the problem is to find the area of the shaded region. In order to solve this problem, we consider three special cases of f (x) as rectangular region , triangular region and trapezoidal region. The area of these regions = base × average height In general for any functio ...
... shaded region in Fig.27.3. Now the problem is to find the area of the shaded region. In order to solve this problem, we consider three special cases of f (x) as rectangular region , triangular region and trapezoidal region. The area of these regions = base × average height In general for any functio ...
Single Digits: In Praise of Small Numbers
... © Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. ...
... © Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. ...
Subtraction of Convex Sets and Its Application in E
... Nurminski, E.A. (1982) Subtraction of Convex Sets and Its Application in E-Subdifferential Calculus. IIASA Working Paper. IIASA, Laxenburg, Austria, WP-82-083 Copyright © 1982 by the author(s). http://pure.iiasa.ac.at/1933/ Working Papers on work of the International Institute for Applied Systems A ...
... Nurminski, E.A. (1982) Subtraction of Convex Sets and Its Application in E-Subdifferential Calculus. IIASA Working Paper. IIASA, Laxenburg, Austria, WP-82-083 Copyright © 1982 by the author(s). http://pure.iiasa.ac.at/1933/ Working Papers on work of the International Institute for Applied Systems A ...
Labeled Factorization of Integers
... factorizations which also employed non-adjacent pairings of factors. The procedure for generating F (n) in this context is OrdFactor, which may be viewed as the union of the applications of Factor to each member of F P (n) with the further restriction that only adjacent factors are merged, but gene ...
... factorizations which also employed non-adjacent pairings of factors. The procedure for generating F (n) in this context is OrdFactor, which may be viewed as the union of the applications of Factor to each member of F P (n) with the further restriction that only adjacent factors are merged, but gene ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.