complex numbers - Siby Sebastian
... important because it made the whole idea of a complex number more acceptable. In particular, this visualization helped "imaginary" and "complex" numbers become accepted in mainstream mathematics as a natural extension to negative numbers along the real line. ...
... important because it made the whole idea of a complex number more acceptable. In particular, this visualization helped "imaginary" and "complex" numbers become accepted in mainstream mathematics as a natural extension to negative numbers along the real line. ...
Chapter 5 - Scarsdale Public Schools
... ○ 2. Zeros. There are three classes of zeros: ■ A. Leading zeros are zeros that precede all of the nonzero digits. They never count as significant figures ■ B. Captive zeros are zeros that fall between nonzero digits. They always count as significant figures. ■ C. Trailing zeros are zeros at the rig ...
... ○ 2. Zeros. There are three classes of zeros: ■ A. Leading zeros are zeros that precede all of the nonzero digits. They never count as significant figures ■ B. Captive zeros are zeros that fall between nonzero digits. They always count as significant figures. ■ C. Trailing zeros are zeros at the rig ...
Name - Home [www.petoskeyschools.org]
... Composite Numbers – are divisible by more than two numbers. Tell whether each number is prime or composite. (hint: use the divisibility rules!) ...
... Composite Numbers – are divisible by more than two numbers. Tell whether each number is prime or composite. (hint: use the divisibility rules!) ...
Dividing with Significant Figures
... result is limited by the least accurate measurement involved in the calculation. • Division ▫ After dividing the numbers, you then round the result off so it has the same number of significant figures as the component with the smallest number of significant figures. ...
... result is limited by the least accurate measurement involved in the calculation. • Division ▫ After dividing the numbers, you then round the result off so it has the same number of significant figures as the component with the smallest number of significant figures. ...
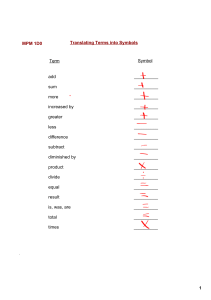
1 MPM 1D0 Translating Terms into Symbols Term Symbol add
... 16. Sixteen subtracted from five times a number 16._______________ equals the number plus four 17. Twice a number decreased by eight is zero 17._______________ 18. A number is equal to fifty less nine times the 18._______________ number 19. The product of twic ...
... 16. Sixteen subtracted from five times a number 16._______________ equals the number plus four 17. Twice a number decreased by eight is zero 17._______________ 18. A number is equal to fifty less nine times the 18._______________ number 19. The product of twic ...
Logic and Proof Exercises Question 1 Which of the following are true
... Use an algebraic proof to prove each of the following true statements. (a) The product of two odd numbers is an odd number. (b) The product of two square numbers is a square number. (A square number is an integer which is the result of squaring another integer. For example, 4 is a square number beca ...
... Use an algebraic proof to prove each of the following true statements. (a) The product of two odd numbers is an odd number. (b) The product of two square numbers is a square number. (A square number is an integer which is the result of squaring another integer. For example, 4 is a square number beca ...
Section 3.2: Direct Proof and Counterexample 2
... (ii ) The sum and difference of two odd integers is even but the product of two odd integers is odd (iii ) The product of an even and odd integer is even (iv ) The sum of an odd and even integer is odd (v ) The difference of an odd and even integer is odd (vi ) The difference of an even and odd inte ...
... (ii ) The sum and difference of two odd integers is even but the product of two odd integers is odd (iii ) The product of an even and odd integer is even (iv ) The sum of an odd and even integer is odd (v ) The difference of an odd and even integer is odd (vi ) The difference of an even and odd inte ...
Discussion
... We know this is not a proof. Considering these questions could lead to an exploration of the sum of the first n natural numbers. For example, suppose that n = 16. One could begin by adding the numbers (i.e. 1 + 2 + 3 + … + 16). However, one way to add the numbers, using the both the commutative and ...
... We know this is not a proof. Considering these questions could lead to an exploration of the sum of the first n natural numbers. For example, suppose that n = 16. One could begin by adding the numbers (i.e. 1 + 2 + 3 + … + 16). However, one way to add the numbers, using the both the commutative and ...
2.2 Factors and Prime Factorization
... 3. Find the prime factorization of a number using factor trees and the division method Prime Factorization of a number—is the factorization in which all the factors are prime numbers. Divisibility Tests: A whole number is divisible by • 2 if the last digit is even. • 3 if the sum of the digit ...
... 3. Find the prime factorization of a number using factor trees and the division method Prime Factorization of a number—is the factorization in which all the factors are prime numbers. Divisibility Tests: A whole number is divisible by • 2 if the last digit is even. • 3 if the sum of the digit ...
27HYD13_Layout 1
... three thousand, one For all hundred eleven comeptative 3. Ans: b exams 4. Ans: d Explanation: If a number has 0, 2, 4, 6 or 8 in its unit's place, then, it is completely divided by 2 Since the units digit in the given number is two, it is divisible by 2. If the sum of all the digits in a number is d ...
... three thousand, one For all hundred eleven comeptative 3. Ans: b exams 4. Ans: d Explanation: If a number has 0, 2, 4, 6 or 8 in its unit's place, then, it is completely divided by 2 Since the units digit in the given number is two, it is divisible by 2. If the sum of all the digits in a number is d ...
The Peano Axioms - Stony Brook Mathematics
... We should remark that some versions of the Peano Axioms begin with the number 1 rather than 0, and some authors refer to the set defined about as the “whole numbers”, and use the term “natural number” to refer to the nonzero whole numbers. In fact, Peano’s original formulation used 1 as the “first” ...
... We should remark that some versions of the Peano Axioms begin with the number 1 rather than 0, and some authors refer to the set defined about as the “whole numbers”, and use the term “natural number” to refer to the nonzero whole numbers. In fact, Peano’s original formulation used 1 as the “first” ...
Recurrence relation
... Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a (mental or spoken) counter by a unit for every element of the set, in some order, while marking (or displacing) those elements to avoid visiting t ...
... Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a (mental or spoken) counter by a unit for every element of the set, in some order, while marking (or displacing) those elements to avoid visiting t ...
Notes 1.5 – Factors and Divisibility Patterns
... If the remainder is zero then the number is divisible by the divisor. ...
... If the remainder is zero then the number is divisible by the divisor. ...
Day 11: Investigating Patterns in Factors Grade 7
... • A number is abundant if the sum of all its factors, other than the number itself, is greater than the number. A number is deficient if the sum of all its factors, other than the number itself, is less than the number. Are 12 and 5 abundant or deficient numbers? Pose the question: Are there pattern ...
... • A number is abundant if the sum of all its factors, other than the number itself, is greater than the number. A number is deficient if the sum of all its factors, other than the number itself, is less than the number. Are 12 and 5 abundant or deficient numbers? Pose the question: Are there pattern ...
Octal Numbering System
... To convert decimal to octal is slightly more difficult. The typical method to convert from decimal to octal is repeated division by 8. While we may also use repeated subtraction by the weighted position value, it is more difficult for large decimal numbers. Repeated Division By 8 For this method, di ...
... To convert decimal to octal is slightly more difficult. The typical method to convert from decimal to octal is repeated division by 8. While we may also use repeated subtraction by the weighted position value, it is more difficult for large decimal numbers. Repeated Division By 8 For this method, di ...
Logistics for TLC Team Planning
... Students wrap-up work Partners stand up and read clues, explain thinking, present number. ...
... Students wrap-up work Partners stand up and read clues, explain thinking, present number. ...
Solutions to the Activities in Understanding Numbers in Elementary
... It is not clear that the meaning of multiplication has been explained. More precisely, there are at least two errors: Error 1: It says there are “different” ways to find the total number, so one expects the different ways to be explained in terms of what students already know. Instead, the way on th ...
... It is not clear that the meaning of multiplication has been explained. More precisely, there are at least two errors: Error 1: It says there are “different” ways to find the total number, so one expects the different ways to be explained in terms of what students already know. Instead, the way on th ...
Lecture #13 - February 27, 2004 - Introduction to Floating Point
... situation isn’t improved when the numbers are converted to binary. Rational numbers such as ⅓, which have an infinite number of repeating digits in decimal (0.33333…), also have an infinite number of fraction bits in binary. What is surprising, however, is that some perfectly well behaved rational n ...
... situation isn’t improved when the numbers are converted to binary. Rational numbers such as ⅓, which have an infinite number of repeating digits in decimal (0.33333…), also have an infinite number of fraction bits in binary. What is surprising, however, is that some perfectly well behaved rational n ...
2.2 Factors and Prime Factorization Learning Objectives
... 3. Find the prime factorization of a number using factor trees and the division method Prime Factorization of a number—is the factorization in which all the factors are prime numbers. Divisibility Tests: A whole number is divisible by • 2 if the last digit is even. • 3 if the sum of the digits ...
... 3. Find the prime factorization of a number using factor trees and the division method Prime Factorization of a number—is the factorization in which all the factors are prime numbers. Divisibility Tests: A whole number is divisible by • 2 if the last digit is even. • 3 if the sum of the digits ...
Redemption Answer Key
... 4.1) Show that there exists a natural number M such that for all natural numbers n, n2 + 3n + 1 > M . Attack: This is a there exists proof, so we need to provide a value for M . The inequality is supposed to be true for all values of n, so our value of M should be smaller than any n2 + 3n + 1. A bit ...
... 4.1) Show that there exists a natural number M such that for all natural numbers n, n2 + 3n + 1 > M . Attack: This is a there exists proof, so we need to provide a value for M . The inequality is supposed to be true for all values of n, so our value of M should be smaller than any n2 + 3n + 1. A bit ...
Name: Date - Education With Fun
... a. 2 is the even prime number. b. 4 is the first composite number. c. The smallest odd prime number is 3. d. 1 is the neither prime nor composite number. e. The sum two prime numbers can be even or odd. f. 14 and 15 is a pair of co-prime number. g. H.C.F of two prime numbers is always1. h. 31 and 37 ...
... a. 2 is the even prime number. b. 4 is the first composite number. c. The smallest odd prime number is 3. d. 1 is the neither prime nor composite number. e. The sum two prime numbers can be even or odd. f. 14 and 15 is a pair of co-prime number. g. H.C.F of two prime numbers is always1. h. 31 and 37 ...
MATHMATICS II 1.2 number systems: A number is a mathematical
... Algebraic numbers are those that can be expressed as the solution to a polynomial equation with integer coefficients. The complement of the algebraic numbers are the transcendental numbers. Hyperreal numbers are used in non-standard analysis. The hyperreals, or nonstandard reals (usually denoted as ...
... Algebraic numbers are those that can be expressed as the solution to a polynomial equation with integer coefficients. The complement of the algebraic numbers are the transcendental numbers. Hyperreal numbers are used in non-standard analysis. The hyperreals, or nonstandard reals (usually denoted as ...

![Name - Home [www.petoskeyschools.org]](http://s1.studyres.com/store/data/008961674_1-3e665c35c8e33814d362defc99f8fdcf-300x300.png)