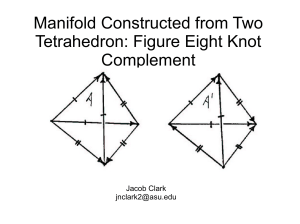
THEOREM 4-3 – Isosceles Triangle Theorem THEOREM 4
... If a triangle is __________________________, then it is also __________________________. ...
... If a triangle is __________________________, then it is also __________________________. ...
On the average distance property of compact connected metric spaces
... Strantzen points out that Stadje's proposition that says a ( X , d ) ~ 8 9 where d is the Euclidean metric and X is any compact convex subset of R n, is wrong. Strantzen gives the correct bound. This has also been pointed out to us by E. Szekeres and G. Szekeres who independently confirmed Strantzen ...
... Strantzen points out that Stadje's proposition that says a ( X , d ) ~ 8 9 where d is the Euclidean metric and X is any compact convex subset of R n, is wrong. Strantzen gives the correct bound. This has also been pointed out to us by E. Szekeres and G. Szekeres who independently confirmed Strantzen ...
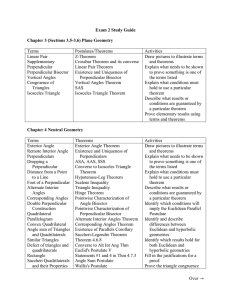
Exam 2 Study Guide
... Postulate Identify and describe differences between Euclidean and hyperbolic geometries Identify which results hold for both Euclidean and hyperbolic geometries Fill in the justifications for a proof. Prove the triangle congruence Over → ...
... Postulate Identify and describe differences between Euclidean and hyperbolic geometries Identify which results hold for both Euclidean and hyperbolic geometries Fill in the justifications for a proof. Prove the triangle congruence Over → ...
Notes 4.5
... congruent to two angles and the corresponding non-included side of a second triangle, then the two triangles are congruent. ...
... congruent to two angles and the corresponding non-included side of a second triangle, then the two triangles are congruent. ...
Geometry - 10.3-10.4 - Side-Splitter Theorem and AA Similarity
... Theorem 45 The AA Theorem If two angles of one triangle are equal to two angles of another triangle, the triangles are similar. Corollary to the AA Theorem Two triangles similar to a third triangle are similar to each other. ...
... Theorem 45 The AA Theorem If two angles of one triangle are equal to two angles of another triangle, the triangles are similar. Corollary to the AA Theorem Two triangles similar to a third triangle are similar to each other. ...
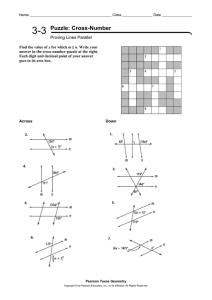
3.3 Prove Lines are ||
... angles Theorem 3.3 If two || lines are cut by a transversal, then the pairs of consecutive interior ∡s are supplementary. Why is this picture similar to the Alternate Interior ∡s picture? ...
... angles Theorem 3.3 If two || lines are cut by a transversal, then the pairs of consecutive interior ∡s are supplementary. Why is this picture similar to the Alternate Interior ∡s picture? ...
Geometry - Ch 10 - Similarity, Side
... Theorem 45 The AA Theorem If two angles of one triangle are equal to two angles of another triangle, the triangles are similar. Corollary to the AA Theorem Two triangles similar to a third triangle are similar to each other. ...
... Theorem 45 The AA Theorem If two angles of one triangle are equal to two angles of another triangle, the triangles are similar. Corollary to the AA Theorem Two triangles similar to a third triangle are similar to each other. ...
7.5 ASA - Van Buren Public Schools
... Explore the Angle-Side-Angle Congruence Theorem through constructions. Explore the Angle-Side-Angle Congruence Theorem on the coordinate plane. Prove the Angle-Side-Angle Congruence Theorem. ...
... Explore the Angle-Side-Angle Congruence Theorem through constructions. Explore the Angle-Side-Angle Congruence Theorem on the coordinate plane. Prove the Angle-Side-Angle Congruence Theorem. ...
File
... Proving the Triangle-Sum Theorem The proof of the Triangle-Sum Theorem requires the use of an auxiliary line. • An auxiliary line is an extra line or segment drawn in a figure to help analyze geometric relationships. • Any properties of an auxiliary line that you draw must be justified ...
... Proving the Triangle-Sum Theorem The proof of the Triangle-Sum Theorem requires the use of an auxiliary line. • An auxiliary line is an extra line or segment drawn in a figure to help analyze geometric relationships. • Any properties of an auxiliary line that you draw must be justified ...
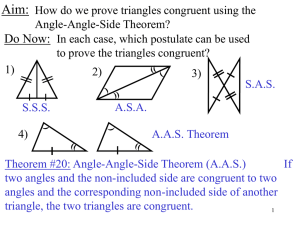
AAS Theorem - Math Story
... Theorem #20: Angle-Angle-Side Theorem (A.A.S.) If two angles and the non-included side are congruent to two angles and the corresponding non-included side of another triangle, the two triangles are congruent. ...
... Theorem #20: Angle-Angle-Side Theorem (A.A.S.) If two angles and the non-included side are congruent to two angles and the corresponding non-included side of another triangle, the two triangles are congruent. ...
November 3
... The hardest part of these six theorems was proving the characterizations of connected and compactness for R. Even if the details of the proof are a bit fuzzy in your head, you should understand that we used in a crucial way that R is complete. Everyone should at least understand the proof of the ge ...
... The hardest part of these six theorems was proving the characterizations of connected and compactness for R. Even if the details of the proof are a bit fuzzy in your head, you should understand that we used in a crucial way that R is complete. Everyone should at least understand the proof of the ge ...
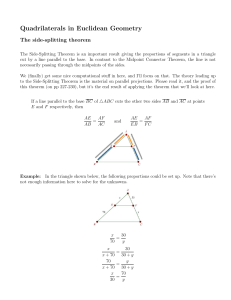
Notes on the Side-Splitting Theorem
... We (finally) get some nice computational stuff in here, and I’ll focus on that. The theory leading up to the Side-Splitting Theorem is the material on parallel projections. Please read it, and the proof of this theorem (on pp 227-230), but it’s the end result of applying the theorem that we’ll look at ...
... We (finally) get some nice computational stuff in here, and I’ll focus on that. The theory leading up to the Side-Splitting Theorem is the material on parallel projections. Please read it, and the proof of this theorem (on pp 227-230), but it’s the end result of applying the theorem that we’ll look at ...
Introduction: What is Noncommutative Geometry?
... Spin(V, q) ,→ GL1(Cl(V, q)) elements v1 · · · v2k prod of even number of vi ∈ V with q(vi) = 1 • ClC(Rn) complexification of Clifford alg of Rn with standard inn prod: unique min dim representation dim ∆n = 2[n/2] ⇒ rep of Spin(n) on ∆n not factor through SO(n) ...
... Spin(V, q) ,→ GL1(Cl(V, q)) elements v1 · · · v2k prod of even number of vi ∈ V with q(vi) = 1 • ClC(Rn) complexification of Clifford alg of Rn with standard inn prod: unique min dim representation dim ∆n = 2[n/2] ⇒ rep of Spin(n) on ∆n not factor through SO(n) ...
File
... OBJECTIVE: I will will draw valid conclusions and will prove angles congruent using congruent complement and supplement theorems. ...
... OBJECTIVE: I will will draw valid conclusions and will prove angles congruent using congruent complement and supplement theorems. ...
PDF
... † This text is available under the Creative Commons Attribution/Share-Alike License 3.0. You can reuse this document or portions thereof only if you do so under terms that are compatible with the CC-BY-SA license. ...
... † This text is available under the Creative Commons Attribution/Share-Alike License 3.0. You can reuse this document or portions thereof only if you do so under terms that are compatible with the CC-BY-SA license. ...
M 333 L Fall 2002 Solutions to Homework #2
... 5. In proving the converse, you must also divide the proof into two cases: Case 1, which assumes that P is on line segment AB (and thus is the midpoint of line segment AB ) and Case 2, which assumes that P is not on the line segment AB (and so some other point, say M, is the midpoint of line segment ...
... 5. In proving the converse, you must also divide the proof into two cases: Case 1, which assumes that P is on line segment AB (and thus is the midpoint of line segment AB ) and Case 2, which assumes that P is not on the line segment AB (and so some other point, say M, is the midpoint of line segment ...
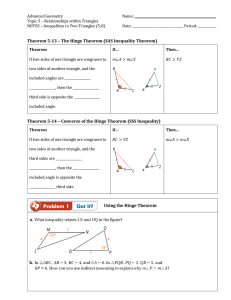
Theorem 5-13 – The Hinge Theorem (SAS Inequality Theorem
... Applying the Hinge Theorem The diagram shows a pair of scissors in two different positions. In which position is the distance between the tips of the two blades greater? Use the Hinge Theorem to justify your answer. ...
... Applying the Hinge Theorem The diagram shows a pair of scissors in two different positions. In which position is the distance between the tips of the two blades greater? Use the Hinge Theorem to justify your answer. ...