Angles In Triangles And Quadrilaterals Year 6
... measurement and, 5 4 using similar triangles big ideas math - 5 4 using similar triangles c if two triangles are similar then their corresponding angles are congruent if two quadrilaterals are similar, 6 angles in quadrilaterals kuta software llc - angles in quadrilaterals date period find the measu ...
... measurement and, 5 4 using similar triangles big ideas math - 5 4 using similar triangles c if two triangles are similar then their corresponding angles are congruent if two quadrilaterals are similar, 6 angles in quadrilaterals kuta software llc - angles in quadrilaterals date period find the measu ...
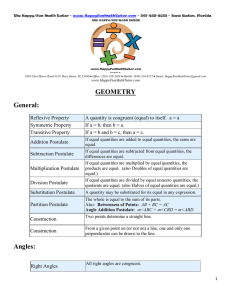
GEOMETRY General: Angles:
... products are equal. (also Doubles of equal quantities are equal.) If equal quantities are divided by equal nonzero quantities, the quotients are equal. (also Halves of equal quantities are equal.) A quantity may be substituted for its equal in any expression. The whole is equal to the sum of its par ...
... products are equal. (also Doubles of equal quantities are equal.) If equal quantities are divided by equal nonzero quantities, the quotients are equal. (also Halves of equal quantities are equal.) A quantity may be substituted for its equal in any expression. The whole is equal to the sum of its par ...