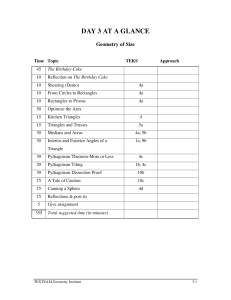
chapter four
... but on two different shapes of equal type. Corresponding Sides are sides that are located in the same position but on two different shapes of equal type. If two triangles are congruent then their Corresponding Angles are congruent. If two triangles are congruent then their Corresponding Sides ...
... but on two different shapes of equal type. Corresponding Sides are sides that are located in the same position but on two different shapes of equal type. If two triangles are congruent then their Corresponding Angles are congruent. If two triangles are congruent then their Corresponding Sides ...
Proving Triangles Congruent
... Does having one pair of sides and a pair of adjacent angles congruent guarantee congruent triangles? Explain your answer. ________________________________ ___________________________________________________________________ ...
... Does having one pair of sides and a pair of adjacent angles congruent guarantee congruent triangles? Explain your answer. ________________________________ ___________________________________________________________________ ...
on three classes of regular toroids
... vertices (and nine faces). (Each vertex is incident with four faces which altogether have a total of nine vertices; for ordinary polyhedra any two of these nine vertices must be distinct.) ...
... vertices (and nine faces). (Each vertex is incident with four faces which altogether have a total of nine vertices; for ordinary polyhedra any two of these nine vertices must be distinct.) ...
Congruence of Triangles
... Break off pairs of ekel sticks of lengths 5 cm, 6 cm and 7 cm respectively. Make two triangles of side lengths 5 cm, 6 cm and 7 cm with these pieces. Do you see that the two triangles have to be congruent? By changing the positions of the pieces of ekel in one triangle, can you create a triangle whi ...
... Break off pairs of ekel sticks of lengths 5 cm, 6 cm and 7 cm respectively. Make two triangles of side lengths 5 cm, 6 cm and 7 cm with these pieces. Do you see that the two triangles have to be congruent? By changing the positions of the pieces of ekel in one triangle, can you create a triangle whi ...
Apollonian network
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.